The dimensions of , where is permittivity of free space and E is electric field, are
The potential at all the points on the axis will be zero
The electric field at all the point on the axis will be zero
The direction of electric field at all points on the axis will be along the axis.
If the ring is placed inside a ubiform extermal electric field then net torque acting on the ring would be zero.
The correct Answer is:A
Potential at any point is a scalequantity.
Position charge negative charge i.e. the net charge is equal to zero. Hence potential is zero. Electric field is a vector quantity so it depends not only distance but also the way of distribution of charge.
Topper's Solved these Questions
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Exercise-03
Explore 1 Video
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Exercise-04
Explore 1 Video
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Exercise-01
Explore 24 Videos
- AIIMS 2019Book:ALLENChapter:AIIMS 2019Exercise:PHYSICS
Explore 40 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE (J-A)
Explore 6 Videos
Similar Questions
The dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
View SolutionThe dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
View SolutionThe dimensions of 12ε0E2(ε0= permittivity of free space, E= electric field) is
View SolutionThe dimensions of (μ0ε0)−1/2 are
View SolutionThe dimensions of ε0μ0 are
View SolutionA wire of length L= 20 cm is bent into a semicircular arc and the two equal halves of the arc are uniformly charged with charges +Q and −Q as shown in the figure. The magnitude of the charge on each half is |Q|=103ε0, where ε0 is the permittivity of free the space. The net electric field at the center O is
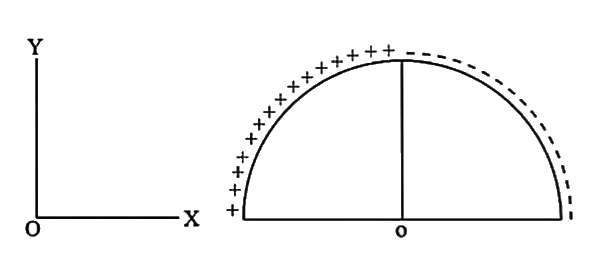
View SolutionThe dimensions of 12∈0E2 (∈0: permittivity of free space, E: electric field) is-
View SolutionThe quantity X=ε0LVt where ε0 is the permittivity of free space, L is length, V is the potential difference and t is time. The dimensions of X are the same as that of
View SolutionA quantity X is given by ε0LΔVΔt, where ε0 is the permittivity of free space L is a length ΔV is a potnetial difference and Δ is a time internval. The dimensional forumla to X is the same as that of
View Solutionε0E2 has the dimensions of
(ε0= permittivity of free space, E= electric field)
Here k= Boltzmann consant
T= absolute temperature
R= universal gas constant.
View Solution