The dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
MLT−1
ML2T−2
ML−1T−2
ML2T−1
The correct Answer is:C
To find the dimension of the expression 12ϵ0E2, where ϵ0 is the permittivity of free space and E is the electric field, we can follow these steps:
Step 1: Identify the dimensions of ϵ0
The permittivity of free space ϵ0 has the dimensions:
(ϵ0)=M−1L−3T4A2
Step 2: Identify the dimensions of the electric field E
The electric field E has the dimensions:
(E)=MLT−2A−1
Step 3: Calculate the dimensions of E2
To find the dimensions of E2, we square the dimensions of E:
(E2)=(MLT−2A−1)2=M2L2T−4A−2
Step 4: Combine the dimensions of ϵ0 and E2
Now, we can combine the dimensions of ϵ0 and E2 in the expression 12ϵ0E2:
(12ϵ0E2)=(ϵ0)⋅(E2)=(M−1L−3T4A2)⋅(M2L2T−4A−2)
Step 5: Perform the multiplication
Now, we multiply the dimensions:
(12ϵ0E2)=M−1+2L−3+2T4−4A2−2
This simplifies to:
(12ϵ0E2)=M1L−1T0A0
Step 6: Write the final dimension
Thus, the final dimension of 12ϵ0E2 is:
(12ϵ0E2)=M1L−1
Summary of the Solution
The dimension of 12ϵ0E2 is M1L−1.
---
The permittivity of free space ϵ0 has the dimensions:
(ϵ0)=M−1L−3T4A2
The electric field E has the dimensions:
(E)=MLT−2A−1
To find the dimensions of E2, we square the dimensions of E:
(E2)=(MLT−2A−1)2=M2L2T−4A−2
Now, we can combine the dimensions of ϵ0 and E2 in the expression 12ϵ0E2:
(12ϵ0E2)=(ϵ0)⋅(E2)=(M−1L−3T4A2)⋅(M2L2T−4A−2)
Now, we multiply the dimensions:
(12ϵ0E2)=M−1+2L−3+2T4−4A2−2
This simplifies to:
(12ϵ0E2)=M1L−1T0A0
Thus, the final dimension of 12ϵ0E2 is:
(12ϵ0E2)=M1L−1
The dimension of 12ϵ0E2 is M1L−1.
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Multiple correct Answer Type
Explore 8 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Fill In The Blanks
Explore 4 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Knowledge Check
The unit of permittivity of free space ε0 is:
AFaradBWeberCC2N−1m−2DC2N−1m−1
The dimensions of (μ0ε0)−1/2 are
View SolutionThe dimensions of ε0μ0 are
View Solutionε0E2 has the dimensions of
(ε0= permittivity of free space, E= electric field)
Here k= Boltzmann consant
T= absolute temperature
R= universal gas constant.
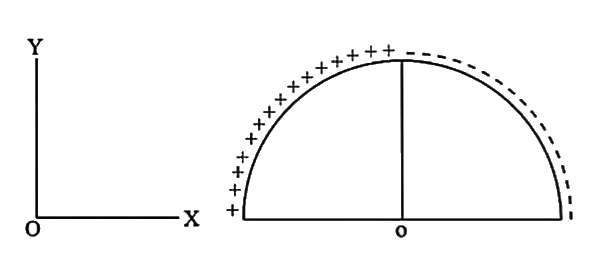
View SolutionA wire of length L= 20 cm is bent into a semicircular arc and the two equal halves of the arc are uniformly charged with charges +Q and −Q as shown in the figure. The magnitude of the charge on each half is |Q|=103ε0, where ε0 is the permittivity of free the space. The net electric field at the center O is
View SolutionThe quantity X=ε0LVt where ε0 is the permittivity of free space, L is length, V is the potential difference and t is time. The dimensions of X are the same as that of
View SolutionWhich of the following does not have the dimensions of velocity ? ( Given ε0 is the permittivity of free space , μ0 is the permeability of free space , v is frequency , λ is wavelength , P is the pressure , and ρ is density , k is wave number , ω is the the angular frequency) (1)ω k (2)vλ (3)1/√ε0μ0 (4)√Pρ
View SolutionThe dimensional formula of 12ε0E2 is (E=electric field)
View Solution

