A student performs an experiment to determine the Young's modulus of a wire, exactly long, by Searle's method. In a partcular reading, the student measures the extension in the length of the wire to be +- 0.05mm1.0kg04mm+-0.01mmg=9.8m//s^(2) (exact). the Young's modulus obtained from the reading is
The correct Answer is:B
To determine the Young's modulus of a wire using the given data, we will follow these steps:
Step 1: Understand the formula for Young's Modulus
Young's modulus (Y) is defined as the ratio of stress to strain. The formula can be expressed as:
Y=StressStrain
Where:
- Stress = FA
- Strain = ΔLL
Step 2: Calculate the Stress
First, we need to calculate the force (F) applied to the wire. The force can be calculated using the weight of the load:
F=m⋅g
Given:
- Mass m=1.0kg
- Acceleration due to gravity g=9.8m/s2
Calculating the force:
F=1.0kg×9.8m/s2=9.8N
Next, we need to calculate the cross-sectional area (A) of the wire. The diameter of the wire is given as 0.4mm, which we convert to meters:
d=0.4mm=0.4×10−3m=4×10−4m
The radius r is:
r=d2=4×10−42=2×10−4m
Now, we can calculate the area:
A=πr2=π(2×10−4)2=π×4×10−8≈1.25664×10−7m2
Now we can calculate the stress:
Stress=FA=9.8N1.25664×10−7m2≈7.80×107Pa
Step 3: Calculate the Strain
The original length of the wire L is given as 2m, and the extension ΔL is given as 0.8mm:
ΔL=0.8mm=0.8×10−3m=8×10−4m
Now we can calculate the strain:
Strain=ΔLL=8×10−4m2m=4×10−4
Step 4: Calculate Young's Modulus
Now we can substitute the values of stress and strain into the Young's modulus formula:
Y=StressStrain=7.80×107Pa4×10−4≈1.95×1011Pa
Step 5: Calculate the Uncertainty in Young's Modulus
To find the uncertainty in Young's modulus, we will use the formula for fractional error:
ΔYY=ΔFF+2Δdd+ΔLL
Where:
- ΔF=g⋅Δm=9.8⋅0.05N
- Δd=0.01mm=0.01×10−3m
- ΔL=0.05mm=0.05×10−3m
Calculating each term:
1. ΔF=9.8×0.05=0.49N
2. ΔFF=0.499.8≈0.05
3. Δdd=0.01×10−30.4×10−3=0.025
4. ΔLL=0.05×10−32=0.025
Now substituting into the fractional error formula:
ΔYY=0.05+2(0.025)+0.025=0.125
Now calculating the uncertainty in Young's modulus:
ΔY=Y⋅0.125=(1.95×1011)⋅0.125≈2.44×1010Pa
Final Result
Thus, the Young's modulus obtained from the readings is:
Y≈1.95×1011Pa±2.44×1010Pa
Young's modulus (Y) is defined as the ratio of stress to strain. The formula can be expressed as:
Y=StressStrain
Where:
- Stress = FA
- Strain = ΔLL
First, we need to calculate the force (F) applied to the wire. The force can be calculated using the weight of the load:
F=m⋅g
Given:
- Mass m=1.0kg
- Acceleration due to gravity g=9.8m/s2
F=1.0kg×9.8m/s2=9.8N
d=0.4mm=0.4×10−3m=4×10−4m
The radius r is:
r=d2=4×10−42=2×10−4m
Now, we can calculate the area:
A=πr2=π(2×10−4)2=π×4×10−8≈1.25664×10−7m2
Stress=FA=9.8N1.25664×10−7m2≈7.80×107Pa
The original length of the wire L is given as 2m, and the extension ΔL is given as 0.8mm:
ΔL=0.8mm=0.8×10−3m=8×10−4m
Now we can calculate the strain:
Strain=ΔLL=8×10−4m2m=4×10−4
Now we can substitute the values of stress and strain into the Young's modulus formula:
Y=StressStrain=7.80×107Pa4×10−4≈1.95×1011Pa
To find the uncertainty in Young's modulus, we will use the formula for fractional error:
ΔYY=ΔFF+2Δdd+ΔLL
Where:
- ΔF=g⋅Δm=9.8⋅0.05N
- Δd=0.01mm=0.01×10−3m
- ΔL=0.05mm=0.05×10−3m
1. ΔF=9.8×0.05=0.49N
2. ΔFF=0.499.8≈0.05
3. Δdd=0.01×10−30.4×10−3=0.025
4. ΔLL=0.05×10−32=0.025
ΔYY=0.05+2(0.025)+0.025=0.125
ΔY=Y⋅0.125=(1.95×1011)⋅0.125≈2.44×1010Pa
Thus, the Young's modulus obtained from the readings is:
Y≈1.95×1011Pa±2.44×1010Pa
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Multiple correct Answer Type
Explore 8 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Fill In The Blanks
Explore 4 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A student measured the diameter of a wire using a screw gauge with least count 0.001cm and listed the measurement. The correct measurement is
View SolutionA wire of length 15m and diameter 4 mm elongates 0.3mm when stretched by weigth of 2.20kg. Calulate the Young's modulus of the material of the wire.
View SolutionA cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
View SolutionA wire 4m long 0.3 mm diameter is streteched by a force of 8 kg.wt. If the extension in the length amounts to 1.5 mm, calcualte the energy stored in the wire?
View SolutionWhen a screw gauge of least count 0.01 mm is used to measure the diameter of a wire, the reading on the sleeve is found to be 1 mm and the reading on the thimble is found to be 27 divisions.What is the diameter of the wire in cm ?
View SolutionFor the experimental determination of Young.s modulus of elasticity Y of the material of a given wire by using Searle.s apparatus, the spherometer reading while load increasing and decreasing are tabulated below:
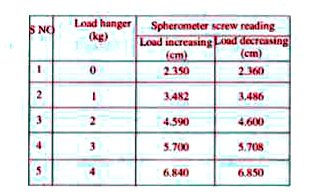
The mean extension for 2kg load is
View SolutionA uniform wire of length 8m and diameter 0.6mm stretched by 4mm under a certain force. If the Poisson's ratio of the material of the wrie is 0.3, calculate the change in diameter of the wire.
View SolutionOne end of a wire 2m long and 0.2 cm^2 in cross section is fixed in a ceiling and a load of 4.8 kg is attached to the free end. Find the extension of the wire. Young modulus of steel =2.0×1011Nm−2. Take g=10ms−2.
View SolutionA screw gauge with a pitch of 1 mm has 100 divisions on its circular scale. What it is used to measure the diameter of a thin wire, the main scale reading is 3 mm and the circular scale reading is 45. If D is the diameter of the wire in mm, then find the value of D.
View SolutionIf the length of wire is (100.0 cm) and radius of wire as measured from screw gauge is (1.00mm) then the specific resistance of wire material is .
View Solution