The dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
[ML2T−2]
[ML−1T−2]
[ML2T−1]
[MLT−1]
The correct Answer is:B
To find the dimension of the term 12ϵ0E2, where ϵ0 is the permittivity of free space and E is the electric field, we can follow these steps:
Step 1: Identify the dimensions of the electric field E.
The electric field E is defined as force per unit charge. The dimension of force is given by:
(F)=MLT−2
The dimension of charge Q is simply Q. Therefore, the dimension of the electric field E can be expressed as:
(E)=(F)(Q)=MLT−2Q=MLT−2Q−1
Step 2: Calculate the dimension of E2.
Now, we need to find the dimension of E2:
(E2)=(MLT−2Q−1)2=M2L2T−4Q−2
Step 3: Identify the dimensions of ϵ0.
The permittivity of free space ϵ0 can be related to the electric field and force. It is defined in terms of the electric field and charge as follows:
\epsilon_0 = \frac{1}{4\pi k} \quad \text{(where k is Coulomb's constant)}
The dimension of ϵ0 can also be derived from the equation of capacitance:
(C)=Q2(F)⇒(ϵ0)=(Q)2(F)(L)=Q2MLT−2L=Q2ML2T−2=M−1L−3T4Q2
Step 4: Combine the dimensions of ϵ0 and E2.
Now we can find the dimension of ϵ0E2:
(ϵ0E2)=(ϵ0)⋅(E2)=(M−1L−3T4Q2)⋅(M2L2T−4Q−2)
Step 5: Simplify the expression.
Now, we simplify the expression:
(ϵ0E2)=M−1L−3T4Q2⋅M2L2T−4Q−2=M2−1L2−3T4−4Q2−2=M1L−1T0Q0=ML−1
Step 6: Final dimension.
Thus, the dimension of 12ϵ0E2 is:
(ML−1)
Conclusion:
The final answer is:
Dimension of 12ϵ0E2=ML−1
The electric field E is defined as force per unit charge. The dimension of force is given by:
(F)=MLT−2
The dimension of charge Q is simply Q. Therefore, the dimension of the electric field E can be expressed as:
(E)=(F)(Q)=MLT−2Q=MLT−2Q−1
Now, we need to find the dimension of E2:
(E2)=(MLT−2Q−1)2=M2L2T−4Q−2
The permittivity of free space ϵ0 can be related to the electric field and force. It is defined in terms of the electric field and charge as follows:
\epsilon_0 = \frac{1}{4\pi k} \quad \text{(where k is Coulomb's constant)}
The dimension of ϵ0 can also be derived from the equation of capacitance:
(C)=Q2(F)⇒(ϵ0)=(Q)2(F)(L)=Q2MLT−2L=Q2ML2T−2=M−1L−3T4Q2
Now we can find the dimension of ϵ0E2:
(ϵ0E2)=(ϵ0)⋅(E2)=(M−1L−3T4Q2)⋅(M2L2T−4Q−2)
Now, we simplify the expression:
(ϵ0E2)=M−1L−3T4Q2⋅M2L2T−4Q−2=M2−1L2−3T4−4Q2−2=M1L−1T0Q0=ML−1
Thus, the dimension of 12ϵ0E2 is:
(ML−1)
The final answer is:
Dimension of 12ϵ0E2=ML−1
Similar Questions
Knowledge Check
The unit of permittivity of free space ε0 is:
AFaradBWeberCC2N−1m−2DC2N−1m−1
The dimensions of (μ0ε0)−1/2 are
View SolutionThe dimensions of ε0μ0 are
View Solutionε0E2 has the dimensions of
(ε0= permittivity of free space, E= electric field)
Here k= Boltzmann consant
T= absolute temperature
R= universal gas constant.
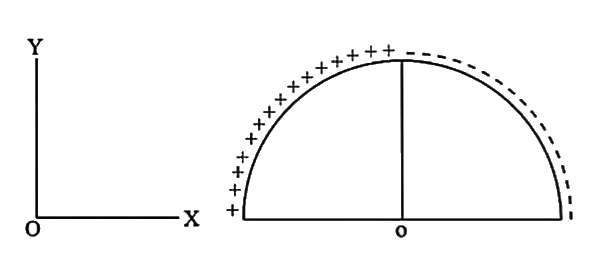
View SolutionA wire of length L= 20 cm is bent into a semicircular arc and the two equal halves of the arc are uniformly charged with charges +Q and −Q as shown in the figure. The magnitude of the charge on each half is |Q|=103ε0, where ε0 is the permittivity of free the space. The net electric field at the center O is
View SolutionThe quantity X=ε0LVt where ε0 is the permittivity of free space, L is length, V is the potential difference and t is time. The dimensions of X are the same as that of
View SolutionWhich of the following does not have the dimensions of velocity ? ( Given ε0 is the permittivity of free space , μ0 is the permeability of free space , v is frequency , λ is wavelength , P is the pressure , and ρ is density , k is wave number , ω is the the angular frequency) (1)ω k (2)vλ (3)1/√ε0μ0 (4)√Pρ
View SolutionThe dimensional formula of 12ε0E2 is (E=electric field)
View Solution
