When force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2

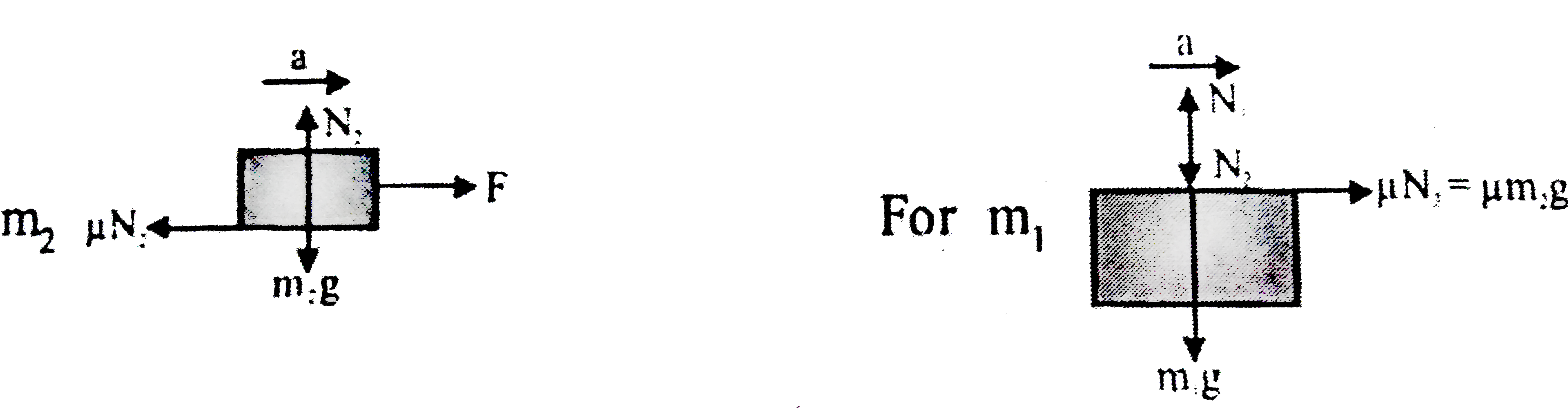
for system : acceleration =Fm1+m2
for m1:μm2g=m1a=m1(Fm1m2),Fmin=(m1+m2)(μ2gm1)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-1)
23 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (S-2)
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
In the pulley arrangement shown in Fig the pulley p2 is movable .Assuming the coefficient of friction between m and surface to be μ the minimum value of M for which m is at rest is

View SolutionThe block each of mass 1kg are placed as shown .They are connected by a string which passes over a smooth (massless) pulley.

There is no friction between m1 and the ground.The coefficient of friction between m1 andm2 is 0.2A force F is applied to m2. Which of the fpllowing statement is/are correct?
View SolutionIn the figure masses m1,m2 and M are kg. 20 Kg, 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.

(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
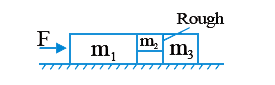
View SolutionThe arrangement shown in the figure, the systme of masses m1,m2 and m3 is being pushed by a force F applied on m1 horizontally. In order to prevent the downwards slipping of m2 between m1 and m3 if coefficient of friction between m2 and m3 is μ and all the other surface are smooth, the minimum value of F :
View SolutionIn the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.

(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.
View SolutionIn the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.

(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.
View Solution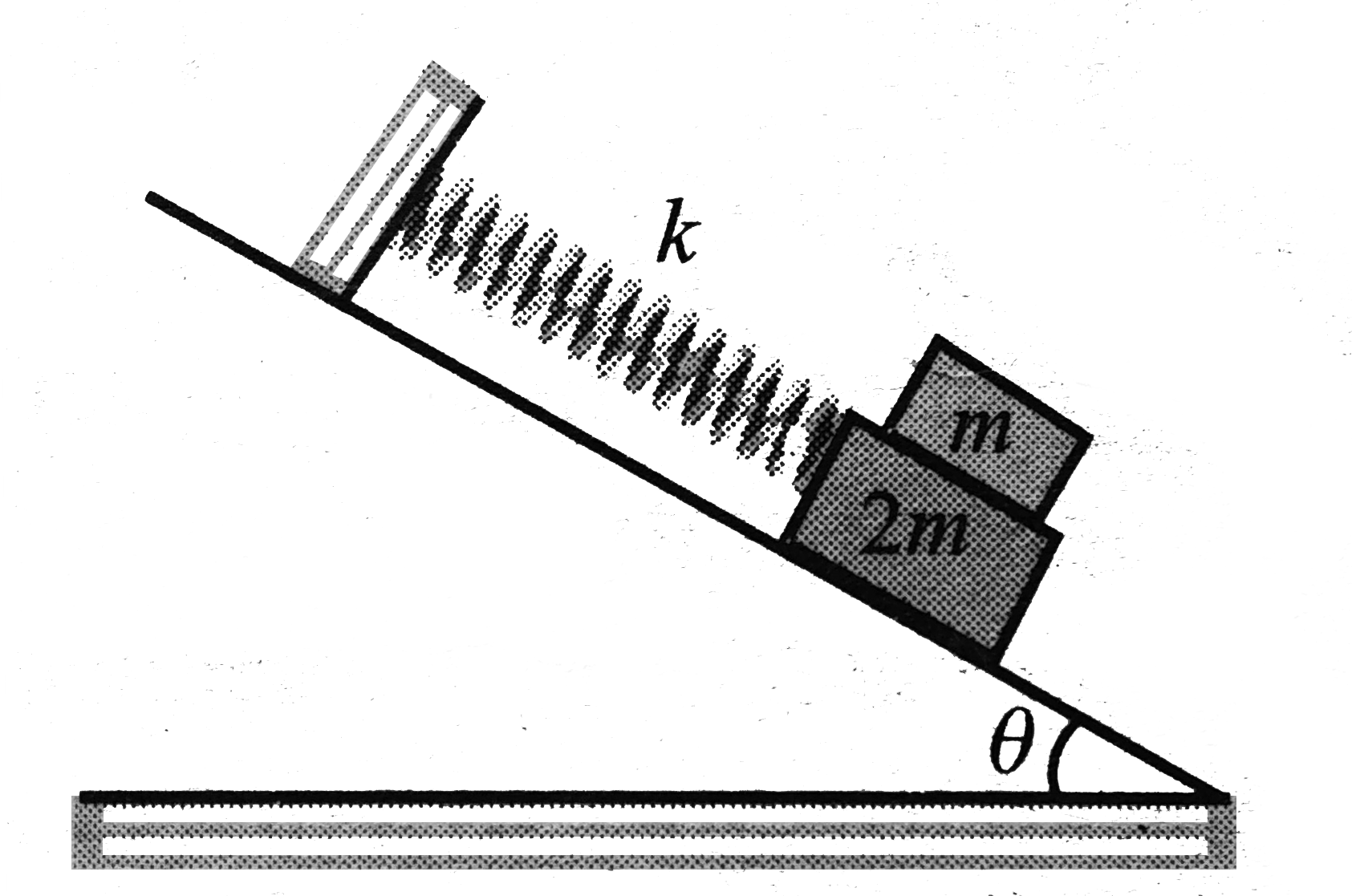
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
View Solution
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
View SolutionA bullet of mass 0.25kg is fired with velocity 302m/s into a block of wood of mass m1=37.5kg. It gets embedded into it. The block m1 is resting on a long block m2 and the horizontal surface on which it is placed is smooth. The coefficient of friction between m1 and m2 is 0.5. Find the displacement of m1 on m2 and the common velocity of m1 and m2. Mass m2=1.25kg.
View SolutionIn figure find the acceleration of m assuming that there is friction between mandM and all other surfaces are smooth and pulleys light and μ=coefficient of friction between mandM

View Solution
