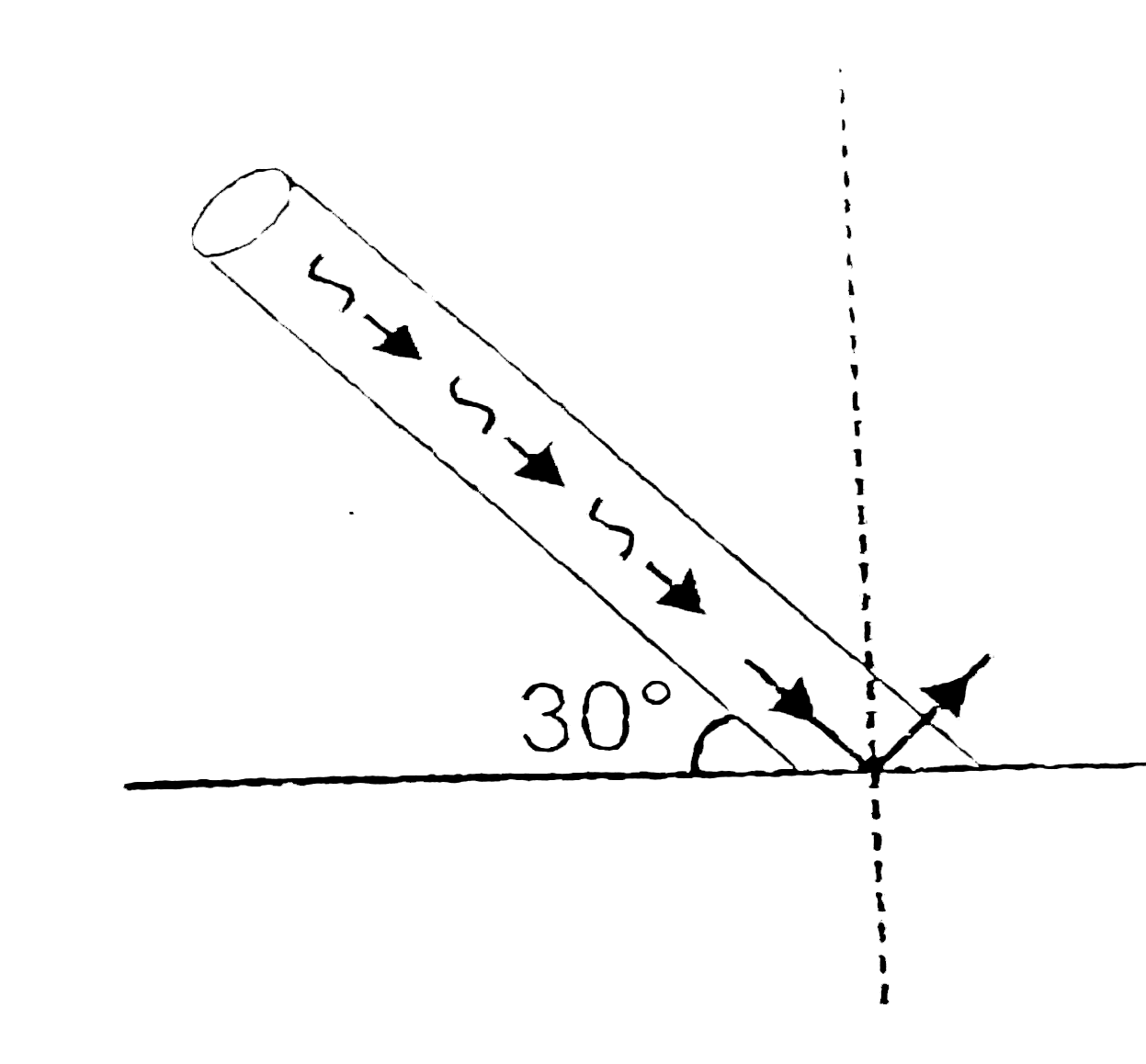
The number of photons (λ=6630Å) that strike per second on a totally reflecting screen (as shown in figure ), so that a force of 1 N is exerted on the screen , is approximately
1023
1027
1025
1026
The correct Answer is:B
F=dpdt⇒F=(2PsinθΔt)
⇒F=2nsinθ [n= number of photon]
⇒1N=2[n]hλsin30∘⇒n=1027
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-02
19 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES
29 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
The number of photons (λ=6630Å) that strike per second on a totoally reflecting screen (as shown in figure), so that a force of 1N is exerted on the screen, is approximentely).
_E01_001_Q01.png)
View Solutionn bullet strikes per second elastically on wall and rebound then what will be the force exerted on the wall by bullets if mass of each bullet is m:-
View SolutionTwo coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
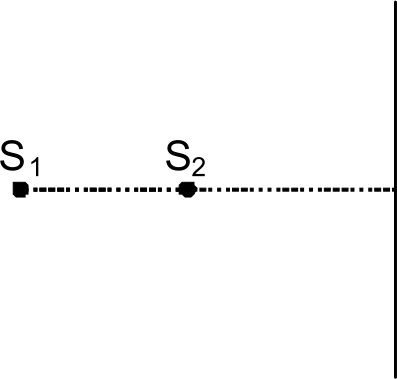
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
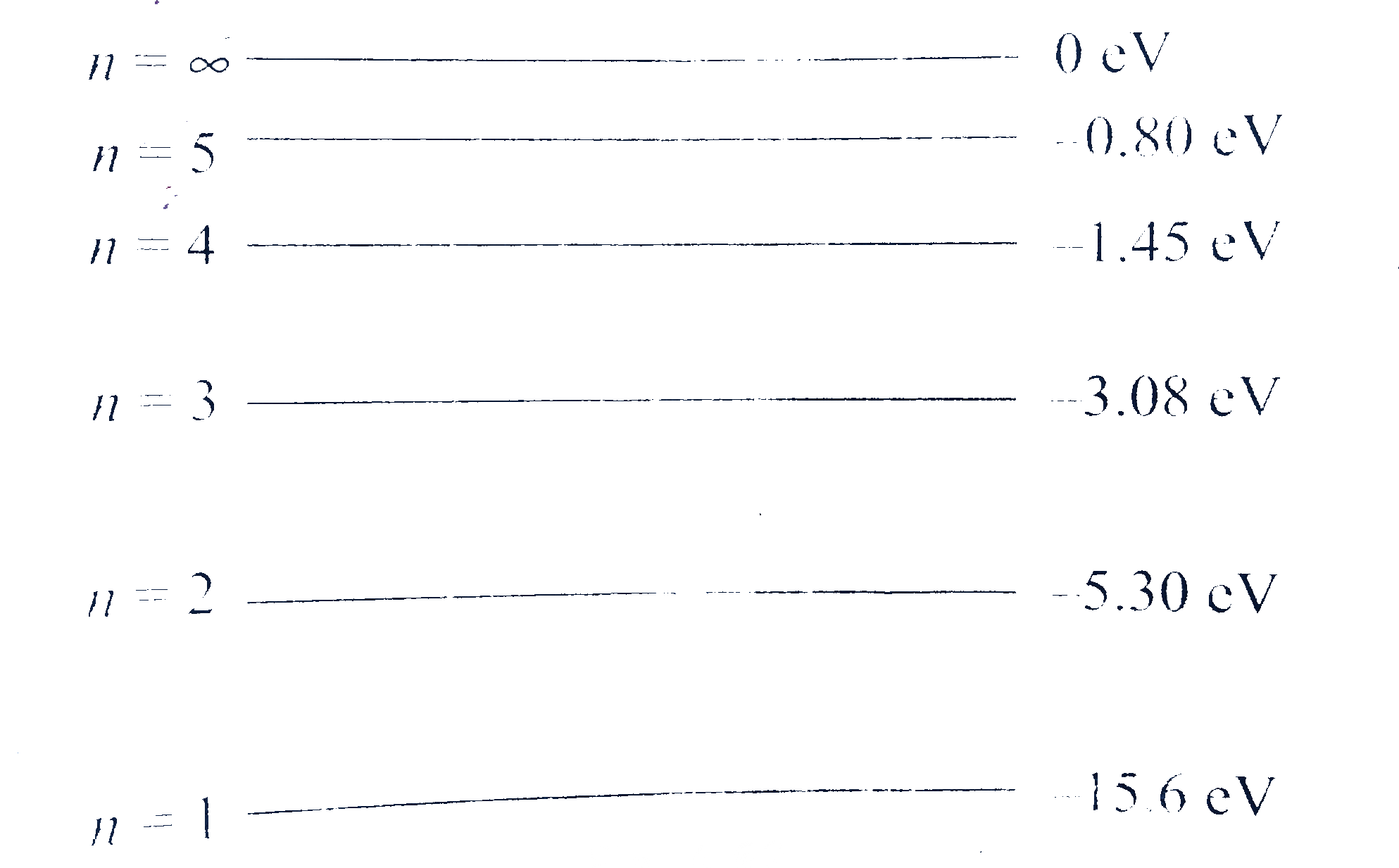
Find the wave number of the photon emitted for the transition n=3→n=1
View SolutionThe number of photons falling per second on a completely darkened plate to produce a force of 6.62×10−5N is 'n'. If the wavelength of the light falling is 5×10−7m, then n= __________ ×1022.
(h=6.62×10−34J−s)
View SolutionPhotons of wavelength λ=662 nm are incident normally on a perfectly reflecting screen. Calculate their number of photons per second falling on the screen such that the exerted force is 1 N.
View SolutionIn a Young's double slit experiment, the light sources is at distance l1=20μm and l2=40μm form the main slit. The light of wavelength lambda = 500nm is incident on slits separated at a distance 10μm. A screen is placed at a distance D = 2 away from the slits as shown in figure. Find
(a) the values of θ relative to the central line where maxima appear on the screen?
(b) how many maxima will appear on the screen?
what should be the minimum thickness of a slab of refractive index 1.5 placed on the path of one of the ray so that minima occurs at C ?
 .
.
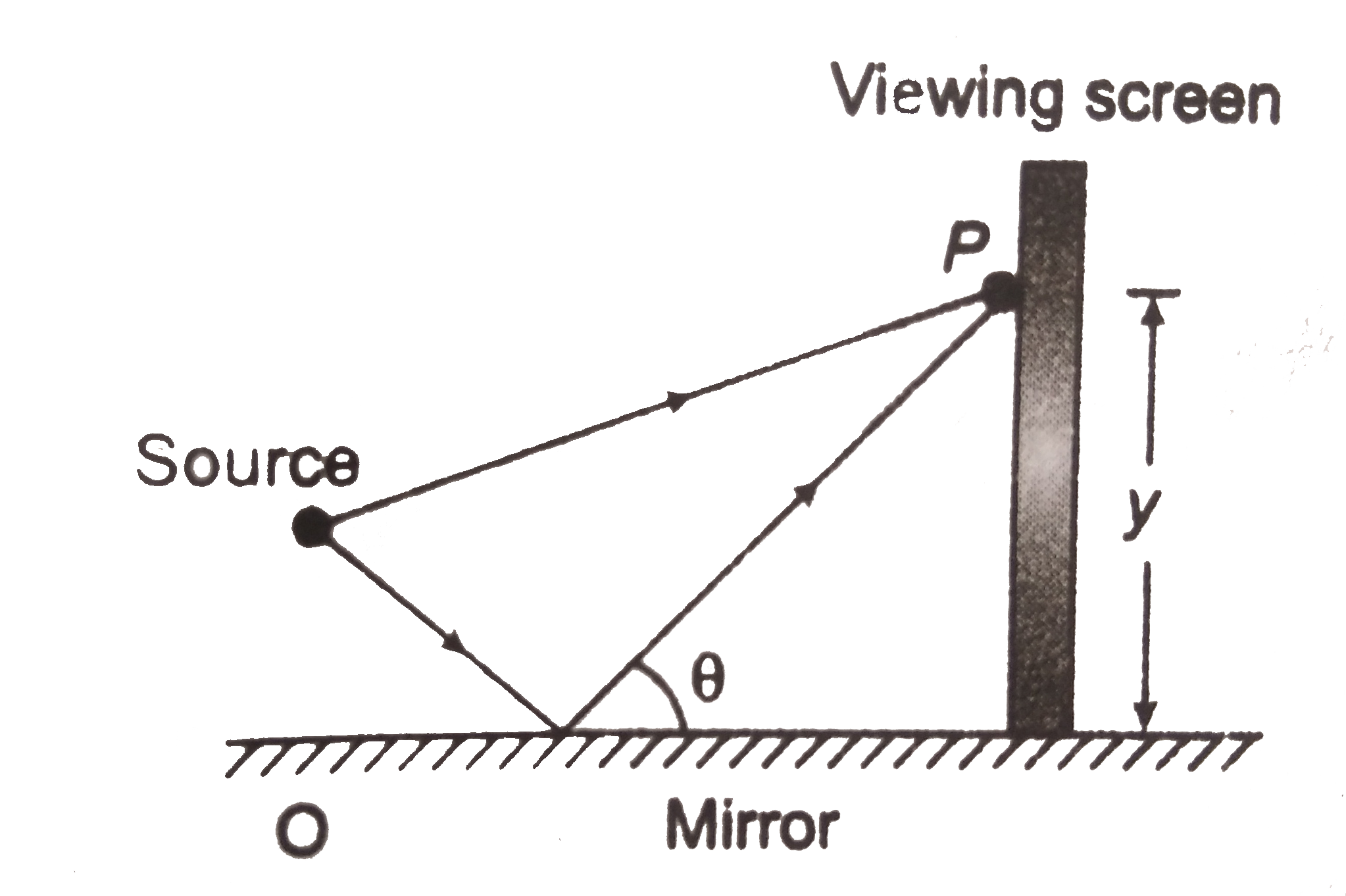
View SolutionInterference effects are produced at point P on a screen as a result of direct rays from a 500 nm source and reflected rays from a mirror, as shown in figure. If the sources is 100m to the left of the screen and 1.00 cm above the mirror, find the distance y (in milimeters) to the first dark band above the mirror.
View SolutionFigure shows a narrow slit S illuminated b a monochromatic light of wavelength λ in a double-slit experiment. In the path of the rays reaching the upper slit S1, a tube to length L is interposed in which the index of reflection of the medium varies linearly as shown in figure . The position of the central maximum in the interference pattern on the screen was displaceed by N fringes. Find the value of N in terms of μ0, L and λ.
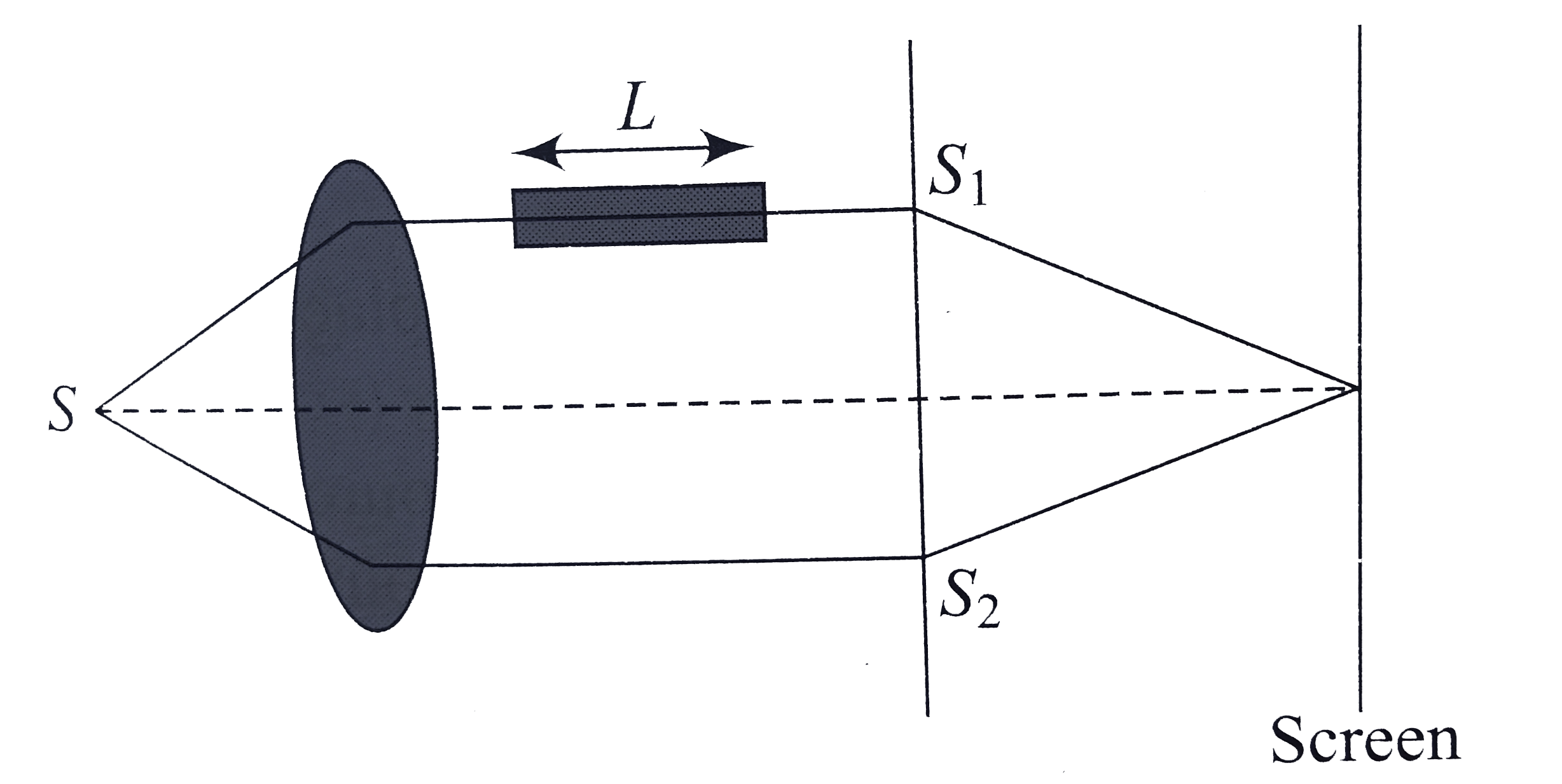
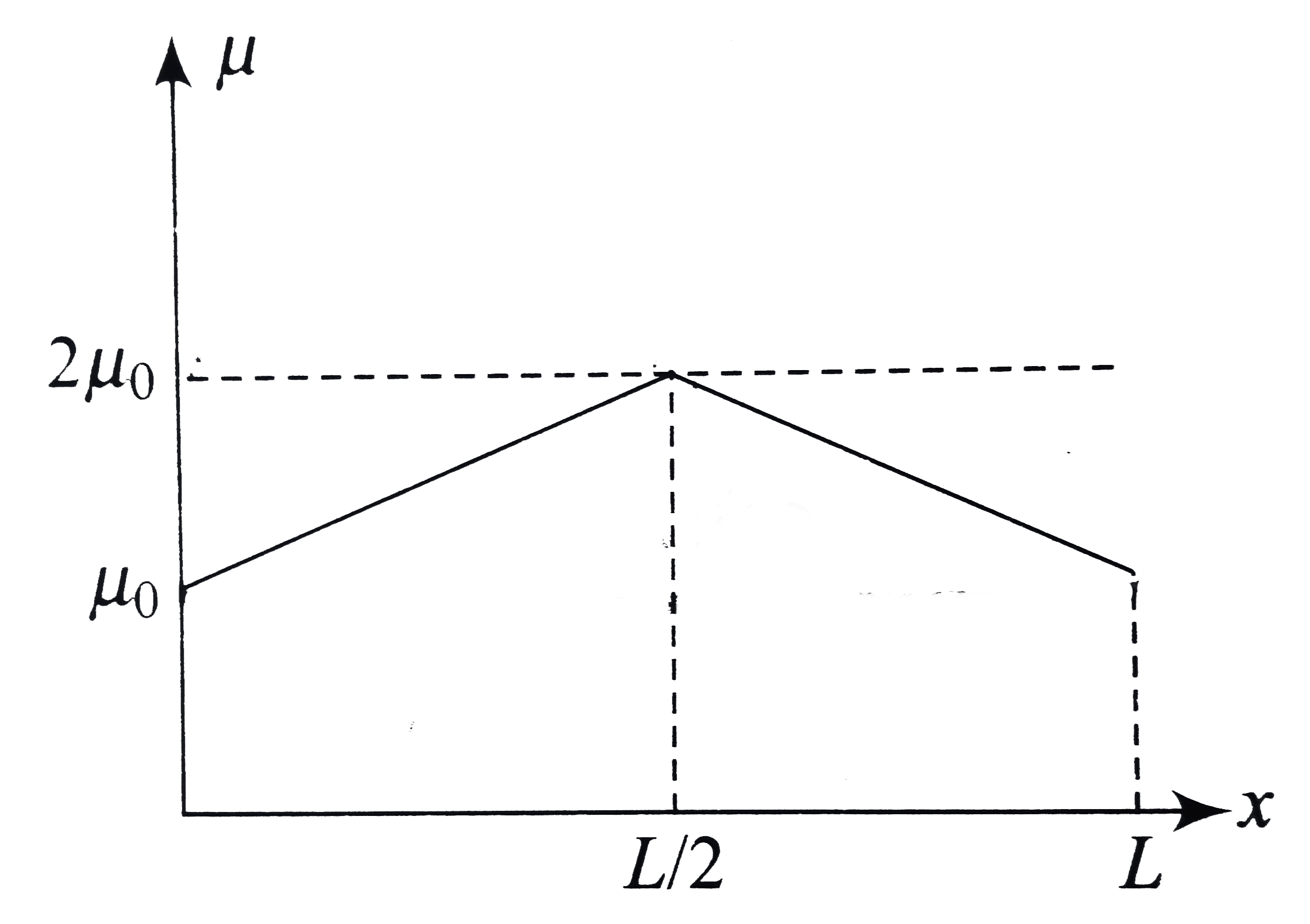
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.

In order to get central maxima at the centre of screen, the thickness of slab required is :
View Solution
