Figure shows a pulley block system in which a block A is hanging one side of pulley and an other side a small bead B of mass m is welded on pulley. The moment of intertia of pulley is I and the sytem is in equilibrium position when bead is at an angle α from the vertical. If the system is slightly disturbed from its equlibrium position, find the time period of its oscillations.
_S01_026_Q01.png)
In equilibrium the net torque on pulley must be ze4ro, thus we have
MgR=mgRsinα
or M=msinα [if mass of block A is assumed tc be M]
Now if block is displace dow by distance A and released, it starts oscillating with amplitude A. Now consider Now if block at distance x below the equilibrium position when it is going down at speed v. Fifure shows the corresponding sitution at this instant and the total energy of oscillating system can be written as
ET=12Mv2+12mv2+12l(vR)2−Mgx+mgR[cosα−cos(θ+α)]
_S01_026_S01.png)
Differenting the abvoe equation w.r.t to time, we get,
dETdt=12M(2vdvdt)+12m(2vdvdt)+121R2(2vdvdt)−Mg(dxdt)+mgR[+sin(0+α)d0dt]=0
⇒Mva=mva+1R2va−Mgv+mgRsin(θ+α)(vR)=0,[asdθdt=ω=vR]
⇒(M+m+IR2)a−Mg−mg[cosα+sinα]=0 [For small angle θ,sinθ=θ,cos1]
⇒(M+m+1R2)a+mgcosα.xR=0[asM=msinαandθ=xR]⇒a=−mgcosαR(M+m+IR2)x
Comparing equation with basic differential equation of SHM, we get the angular frequency of SHM of system
as ω=
⎷mgcosαR(M+m+IR2)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:SOME WORKED OUT EXAMPLES
Explore 29 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-01
Explore 117 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionFind m3 if the system is in equilibrium the incline is smooth and string and pulley are light
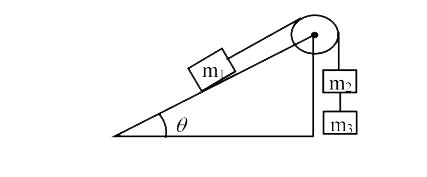
View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

View SolutionA spring of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp at the time of equilibrium is given by
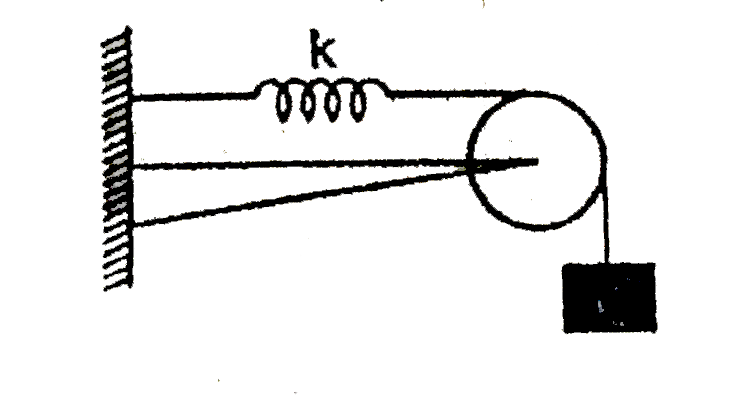
View SolutionFind the acceleration of blocks in fig. The pulley and the string are massless.

View Solution