A transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1 and n2(>n1), θ0, from medium 1 and emerges in medium 2 with refraction angle θtwith a lateral displacement l.
Which of the following statement(s) is (are) true?
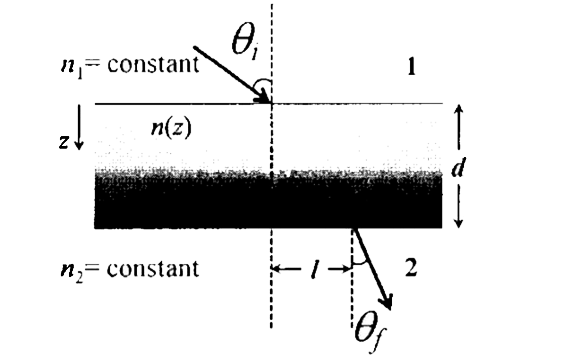
The correct Answer is:ABD
For parallel slab
n1sinθt=n2sinθf
And l depends on refractive angle in slab
∴ l depends on refractive index of slab and independent of n2
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:MATCHING
Explore 2 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE-05 (B)
Explore 35 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
A ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
View SolutionIf a ray of light is incident from rarer medium at an angle 45° on the surface which separates two medium having refractive indices 1 and √2 for rarer and denser medium, then angle of deviation of refractive ray with incident ray is
View Solution
Knowledge Check
Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
A4πdλ(1−1n2sin2θ)1/2+πB4πdλ(1−1n2sin2θ)1/2C4πdλ(1−1n2sin2θ)1/2+π2D4πdλ(1−1n2sin2θ)1/2+2π
Two optical media of refractive indices n1 and n2 contain x and y waves of the same colour in the same thickness. Then their relative refractive index n1/n2
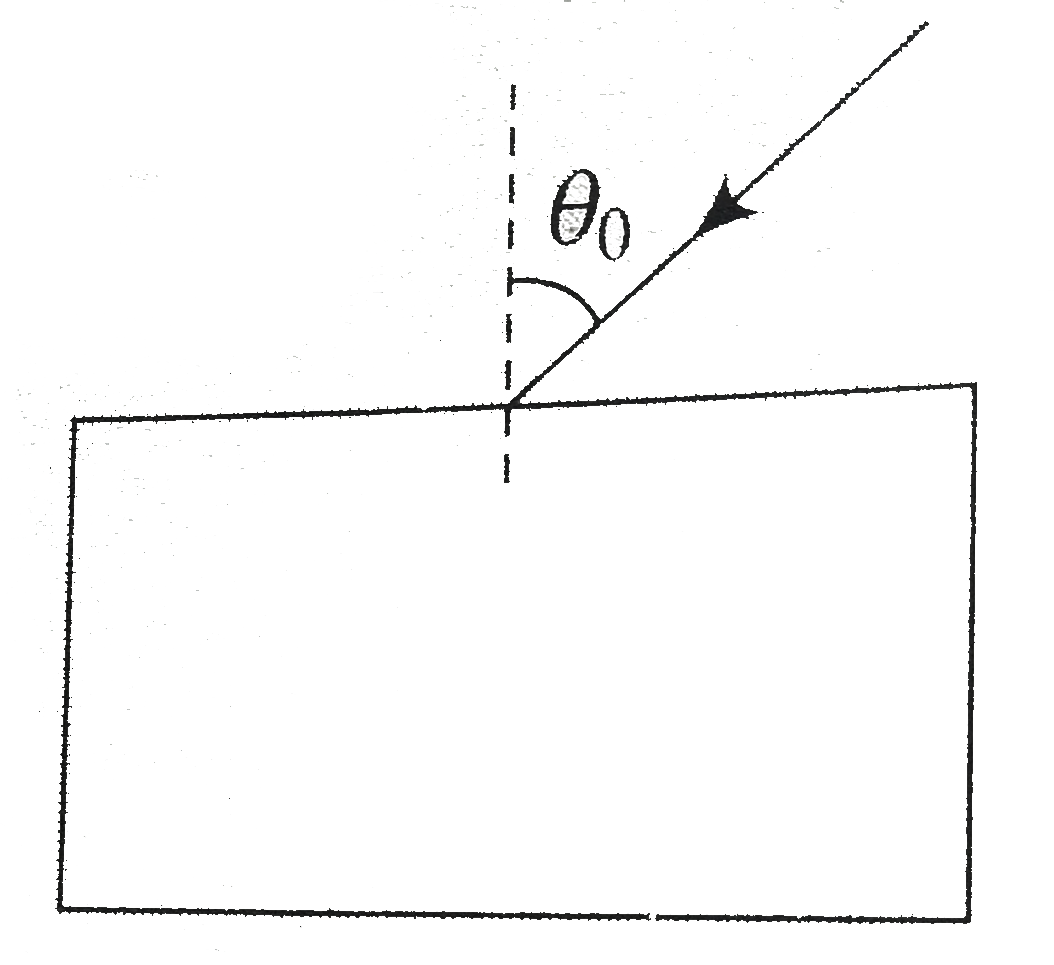
View SolutionA slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
View SolutionConsider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
View SolutionConsider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
View SolutionA spot is placed on the bottom of a slab made of transperent material of refractive index 1.5. The spot is viewed vertically from the top when it seems to be raised by 2 cm. Then, the height of the slab is
View Solution_E01_030_Q01.png)
A light wave travels through three transparent materials of equal thickness rank in order from the highest to lowest the indices of refraction n1,n2 and n3.
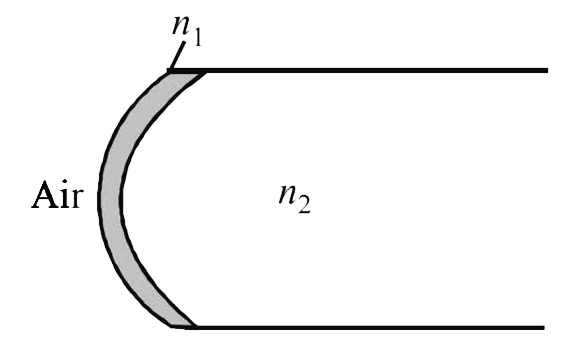
View SolutionA transparent thin film of uniform thickness and refractive index n1=1.4 is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index n2=1.5, as shown in the figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance f1 from the film, while rays of light traversing from glass to air get focused at distance f2 from the film, Then
View Solution
