A rectangular slab ABCD, of refractive index n1 , is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shown in Fig. Find the maximum value of angle of incidence αmax, such that the ray comes out only from the other surface CD.
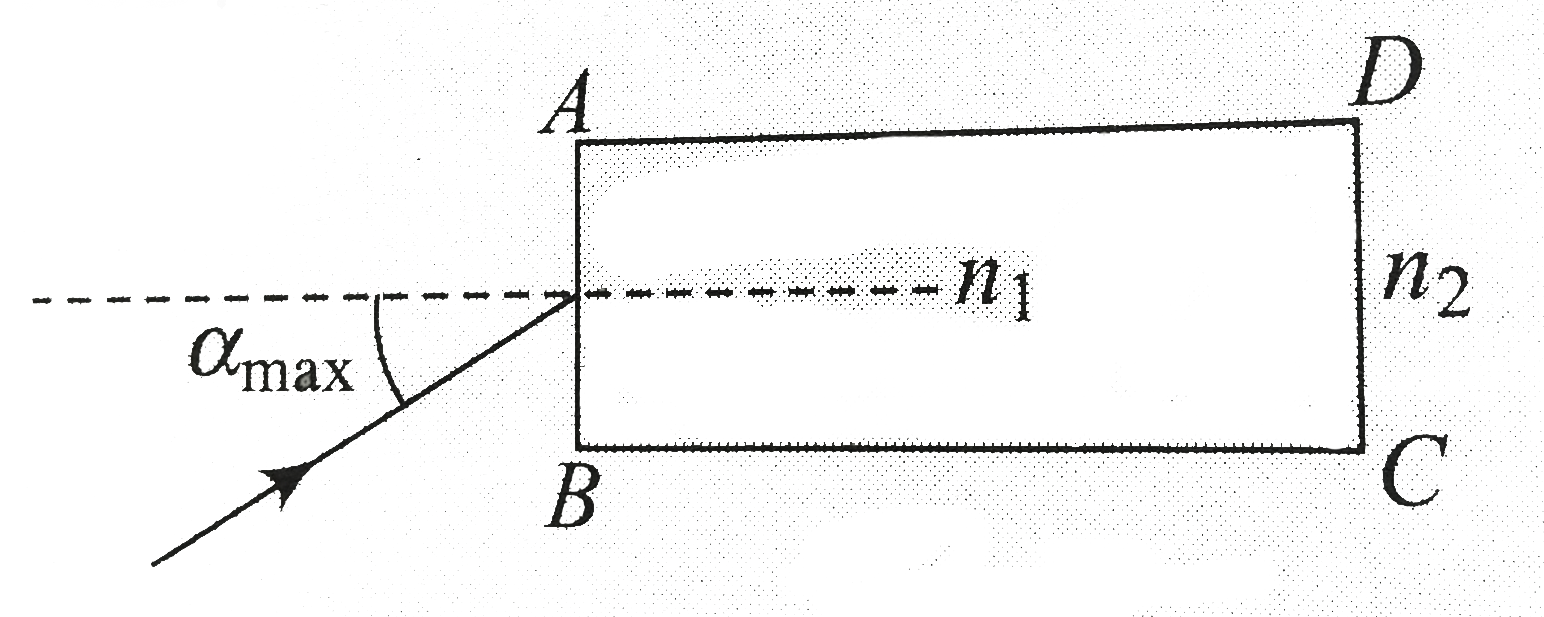
sin−1[n1n2cos(sin−1.n2n1)]
sin−1[n1cos(sin−1.1n2)]
sin−1(n1n2)
sin−1(n2n1)
The correct Answer is:A
Rays come out only form CD , means rays after refraction from AB get total internally reflected at AD .
_E01_205_S01.png)
From the figure :
r1+r2=90∘
r1=90∘−r2
(r1)max=θC
[for total internal reflection at AD]
where sinθC=n2n1orθC=sin−1(n2n1)
∴(r1)max=90∘−θC
Now applying Snell's law at face AB:
n1n2=sinαmaxsin(r1)max=sinαmaxsin(90∘−θC)=sinαmaxcosθC
or sinαmax=n1n2cosθC
∴αmax=sin−1[n1n2cosθC]=sin−1[n1n2cossin−1(n2n1)]
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:MCQ
Explore 5 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:MATCHING
Explore 2 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE-05 (A)
Explore 35 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
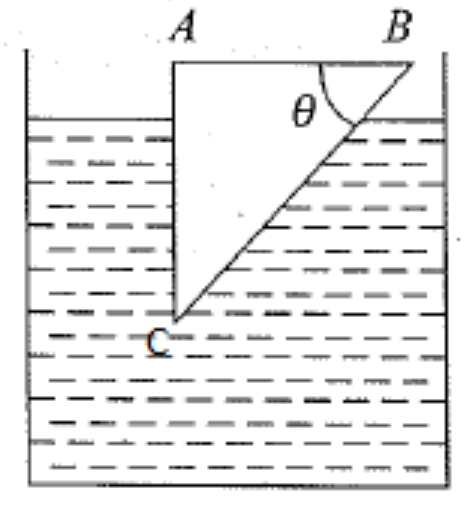
A glass prism of refractive index 1.5 is immersed in water of refractive index 4/3. A light ray incident normally on face AB is totally reflected at face AC if
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
View SolutionA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
View SolutionAB and CD are two slabs. The medium between the slabs has refractive index 2 . Find the minium angle of incidence of Q , so that the ray is totally reflected by both the slabs .
_E01_252_Q01.png)
View SolutionA prism having refractive index √2 and refractive angle 30∘ has one of the refractive surfaces polished. A beam of light incident on the other surfaces will trace its path if the angle of incidence is
View SolutionA cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by
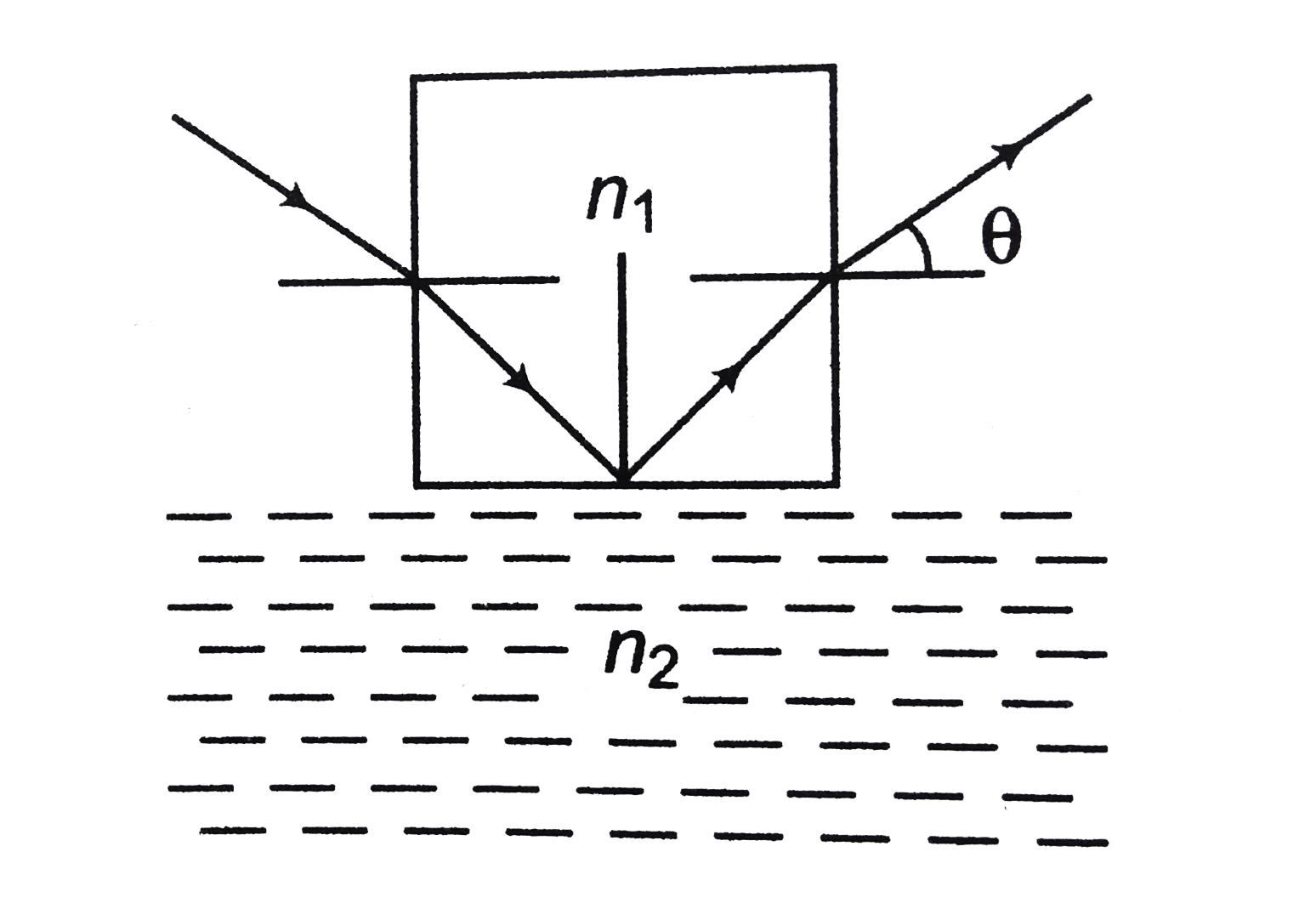
View Solution
Refractive index of a glass cube is √2. A ray of light is incident on left face of the cube as shown. Right face of a glass cube is silvered. If the total deviation suffered by the ray when it comes out of the glass cube is 45n (in degree) then find n:
View SolutionA biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
View SolutionA right angles prism (45∘,90∘,45∘) of refractive index n has a plate of refractive index (n1<n) cemented to its diagonal face. The assembley is in air. A ray is incident on AB.
a. Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle.
b. Assuming n=1.351, calculate the angle of incidence at AB for which the refracted rey passes through the diagonal face undeviated.

View Solution
