A beam of diameter 'd' is incident on a glass hemisphere as shown. If the radius of curvature of the hemisphere is very large in comparison to d, then the diameter of the beam at the base of the hemisphere will be
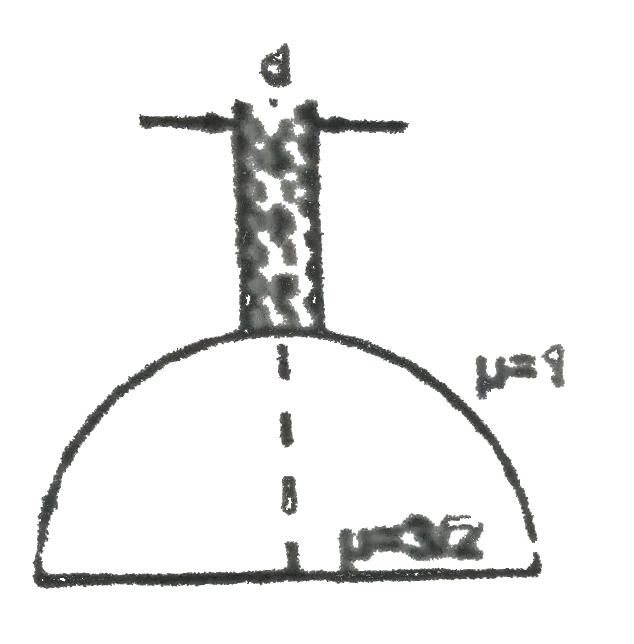
34d
d
d3
23d
The correct Answer is:D
μ1=1,μ2=3/2
(mu_(2))/(v)- (mu_(1))/(mu) = (mu_(2)-mu_(1))/(R)<br>(3)/(2v)- (1)/(-oo)= (3//2-1)/(R) = (1)/(2R)<br>v=3R<br>triangleABE&triangleCDEaresimilar(d)/(3R) = ("x")/(2R)<br>x = (2)/(3)d
_E01_064_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-3
12 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]
23 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE- 01
45 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A light beam of diameter √3R is incident symmetrically on a glass hemisphere of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemisphere.
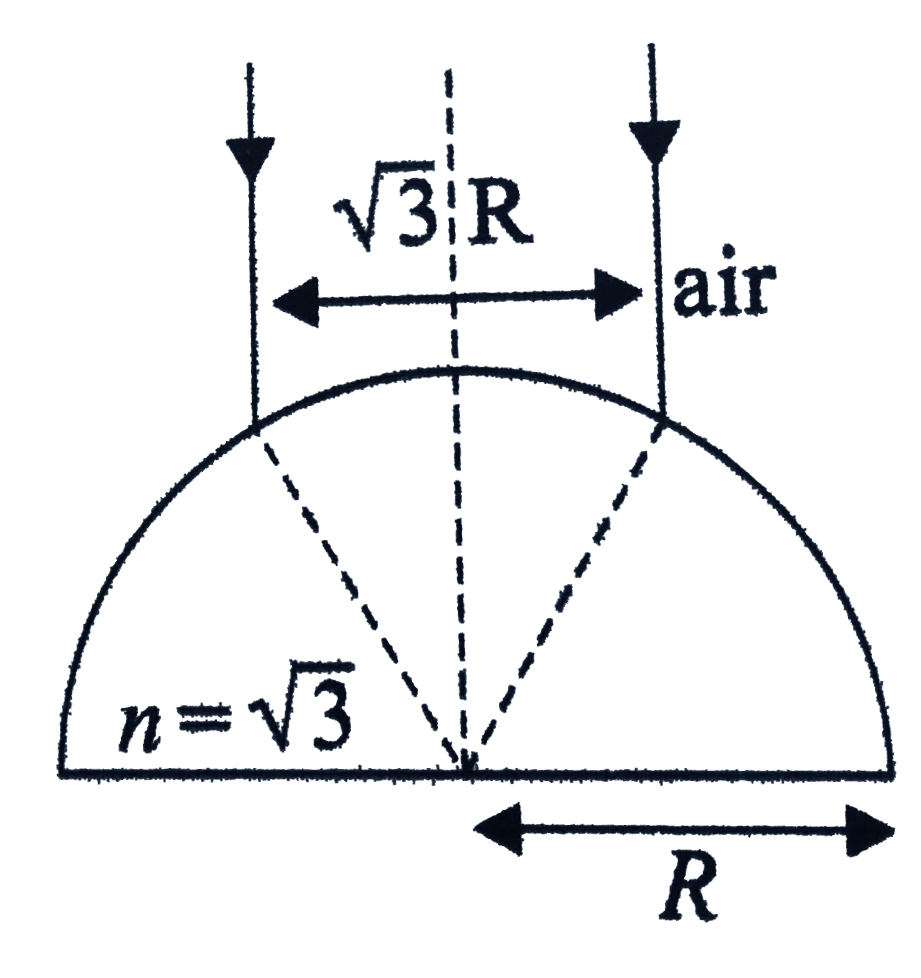
View SolutionA light beam of diameter √3R is incident symmetrically on a glass hemispher of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemispher.

View SolutionVolume and surface area of a solid hemisphere are numerically equal what is the diameter of the hemisphere?
View SolutionA solid glass hemisphere of density d and radius R lies (with curved surface of hemisphere below the flat surface) at the bottom of a tank filled with water of density ρ such that the flat surface of hemisphere is H depth below the liquid surface. Weight of water + tank is W1 and that of hemisphere is'W2. W Then choose the incorrect options
View SolutionThere is a composite solid made up of a circular cylinder and on this a hemisphere is fixed. The refractive index of both the solids is μ, for a laser beam incident as shown. You are given that the radius of the hemisphere is R and the length of the cylinder is 3R/2 . calculate the final divergence of the ray . (μ=√32)

View SolutionFigure shows a transparent hemisphere of radius 3.0 cm made of a material of refractive index 2.0. (a) A narrow beam of parallel rays is incident on the hemisphere as shown in the figure. Are the rays totally reflected at the plane surface ? (b) Find the image formed by the refraction at the first surface. (c) Find the image formed by the reflection or by the refraction at the plane surface. (d) Trace qualitatively the final rays as they come out of the hemisphere.

View SolutionA point source of light is placed at the centre of curvature of a hemispherical surface. The radius of curvature is r and the inner surface is completely reflecting. Find the force on the hemisphere due to the light falling on its if the source emits a power W.
View SolutionA toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21cm and its volume is 2/3 of the volume of the hemisphere, calculate the height of the cone and the surface area of the toy. (Useπ=227).
View SolutionA vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
View SolutionA vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
View Solution
