A point source of light is placed at the centre of curvature of a hemispherical surface. The radius of curvature is r and the inner surface is completely reflecting. Find the force on the hemisphere due to the light falling on its if the source emits a power W.
To solve the problem of finding the force on a hemispherical surface due to light emitted from a point source at its center of curvature, we can follow these steps:
1. Understand the Setup:
- We have a point source of light located at the center of curvature of a hemispherical surface. The radius of curvature is r, and the inner surface of the hemisphere is completely reflecting.
2. Power Emitted by the Source:
- The power emitted by the point source is given as W. This power is distributed uniformly in all directions.
3. Calculate the Area at Distance r:
- The total area over which the light is distributed at a distance r from the source is the surface area of a sphere, which is 4πr2.
4. Energy Incident on a Small Area:
- The energy falling on a small area dA at distance r per unit time can be calculated as:
Energy per unit time on dA=W4πr2⋅dA
5. Calculate the Momentum Change:
- The momentum dP incident on the area dA per unit time is given by:
dP=dEc=W⋅dA4πr2⋅c
- Since the light is reflected, the change in momentum per unit time will be:
ΔP=2⋅dP=2⋅W⋅dA4πr2⋅c=2W⋅dA4πr2⋅c
6. Calculate the Force on Area dA:
- The force dF on the small area dA due to the change in momentum is:
dF=2W⋅dA4πr2⋅c
7. Consider the Geometry:
- The force dF acts along the radius OP at an angle θ with respect to the symmetry axis. The component of dF along the symmetry axis (let's call it OX) is:
dFcosθ=2W⋅dA4πr2⋅ccosθ
8. Integrate Over the Hemisphere:
- To find the total force F on the hemisphere, we need to integrate dFcosθ over the entire hemispherical surface. The projection of dA onto the axis OX gives us:
F=∫dFcosθ=2W4πr2c∫dAcosθ
- The area projected onto the axis is the area of the circle with radius r, which is πr2.
9. Final Calculation:
- Thus, we have:
F=2W4πr2c⋅πr2=2W4c=W2c
Final Answer:
The force on the hemisphere due to the light falling on it is:
F=W2c
- We have a point source of light located at the center of curvature of a hemispherical surface. The radius of curvature is r, and the inner surface of the hemisphere is completely reflecting.
- The power emitted by the point source is given as W. This power is distributed uniformly in all directions.
- The total area over which the light is distributed at a distance r from the source is the surface area of a sphere, which is 4πr2.
- The energy falling on a small area dA at distance r per unit time can be calculated as:
Energy per unit time on dA=W4πr2⋅dA
- The momentum dP incident on the area dA per unit time is given by:
dP=dEc=W⋅dA4πr2⋅c
- Since the light is reflected, the change in momentum per unit time will be:
ΔP=2⋅dP=2⋅W⋅dA4πr2⋅c=2W⋅dA4πr2⋅c
- The force dF on the small area dA due to the change in momentum is:
dF=2W⋅dA4πr2⋅c
- The force dF acts along the radius OP at an angle θ with respect to the symmetry axis. The component of dF along the symmetry axis (let's call it OX) is:
dFcosθ=2W⋅dA4πr2⋅ccosθ
- To find the total force F on the hemisphere, we need to integrate dFcosθ over the entire hemispherical surface. The projection of dA onto the axis OX gives us:
F=∫dFcosθ=2W4πr2c∫dAcosθ
- The area projected onto the axis is the area of the circle with radius r, which is πr2.
- Thus, we have:
F=2W4πr2c⋅πr2=2W4c=W2c
The force on the hemisphere due to the light falling on it is:
F=W2c
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBook:HC VERMA ENGLISHChapter:PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYExercise:objective I
Explore 14 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBook:HC VERMA ENGLISHChapter:PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYExercise:objective II
Explore 7 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBook:HC VERMA ENGLISHChapter:PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYExercise:question for short answer
Explore 13 Videos
- PERMANENT MAGNETSBook:HC VERMA ENGLISHChapter:PERMANENT MAGNETSExercise:Short Answer
Explore 11 Videos
- PHOTOMETRYBook:HC VERMA ENGLISHChapter:PHOTOMETRYExercise:All Questions
Explore 38 Videos
Similar Questions
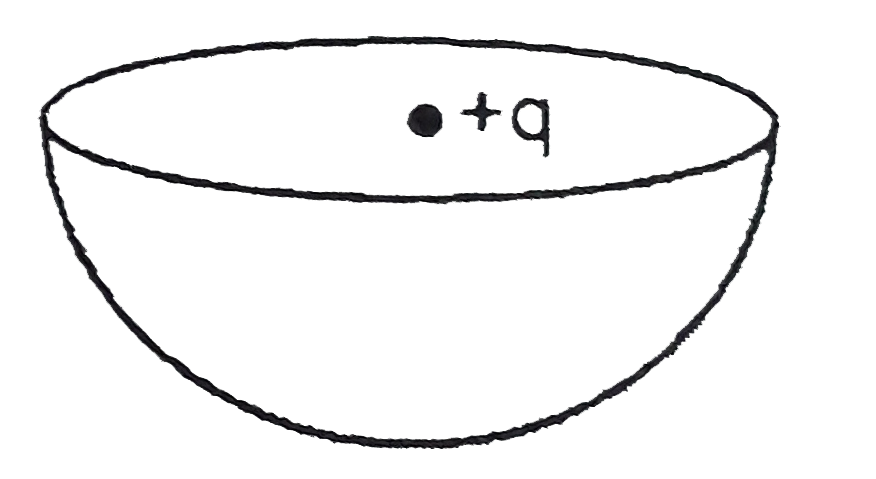
A point charge +q is placed at the centre of curvature of a hemisphere. Find flux through the hemispherical surface.
View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View Solution
Knowledge Check
A point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A2h(μ2−1)1/2B2h(μ2−1)1/2Ch2(μ2−1)1/2Dh(μ2−1)1/2The radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
A2.5DB2DC1.5DD1D
The heat of neutralization for a strong acid by a strong base is a constant
View SolutionFind the flux due to the electric field through the curved surface (R is radius of curvature)

View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA charge Q is placed at the centre of an inaginary hemispherical surface. Using symmetry arguments and the Gauss's law, find the flux of the electric field due to this charge through the surface of the hemisphere (figure ).

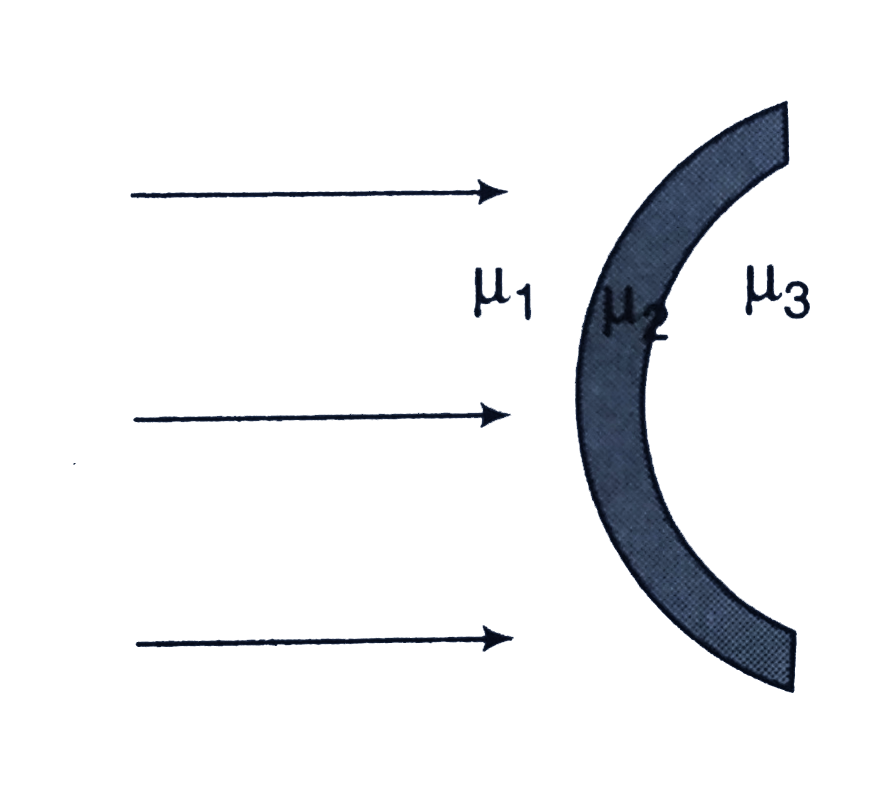
View SolutionIn the figure, light is incident on a thin lens as shown. The radius of curvature for both the surfaces is R. Determine the focal length of this system.
View SolutionThe convex surface of a plano-convex lens is silvered and the radius of curvature of this surface is R. Find the focal length of the system:
View Solution