Two plane mirrors at an angle such that a ray incident on a mirror undergoes a total deviation of 240∘ after two reflections:
the angle between the mirrors is 60∘
the number of images formed by this system will be 5 , if an object is placed symmetrically between the mirrors
the number of images will be 5 if an object is kept unsymmetrical between the mirrors
a ray will retrace its path after 2 successive reflections , if the angle of incidence on one mirror is 60∘
The correct Answer is:A,B,C,D
To solve the problem of finding the angle between two plane mirrors given that a ray incident on one mirror undergoes a total deviation of 240 degrees after two reflections, we can follow these steps:
1. Understand the Concept of Deviation:
- When a ray of light reflects off a mirror, the angle of deviation (D) is defined as the angle between the incident ray and the final ray after reflection. For a single reflection, the deviation is given by the formula:
D=180∘−2i
where i is the angle of incidence.
2. Total Deviation After Two Reflections:
- Since the ray reflects off two mirrors, we need to consider the total deviation after both reflections. If the angle between the mirrors is θ, the total deviation after two reflections can be expressed as:
Dtotal=D1+D2=(180∘−2i1)+(180∘−2i2)
- This simplifies to:
Dtotal=360∘−2(i1+i2)
3. Relate the Angles to the Angle Between Mirrors:
- The angles of incidence i1 and i2 can be related to the angle θ between the mirrors. The relationship is:
i2=θ−i1
- Substituting this into the total deviation equation gives:
Dtotal=360∘−2(i1+(θ−i1))=360∘−2θ
4. Set Up the Equation:
- We know from the problem statement that the total deviation Dtotal is 240 degrees. Thus, we can set up the equation:
360∘−2θ=240∘
5. Solve for θ:
- Rearranging the equation gives:
2θ=360∘−240∘
2θ=120∘
θ=60∘
6. Conclusion:
- The angle between the two mirrors is 60∘.
- When a ray of light reflects off a mirror, the angle of deviation (D) is defined as the angle between the incident ray and the final ray after reflection. For a single reflection, the deviation is given by the formula:
D=180∘−2i
where i is the angle of incidence.
- Since the ray reflects off two mirrors, we need to consider the total deviation after both reflections. If the angle between the mirrors is θ, the total deviation after two reflections can be expressed as:
Dtotal=D1+D2=(180∘−2i1)+(180∘−2i2)
- This simplifies to:
Dtotal=360∘−2(i1+i2)
- The angles of incidence i1 and i2 can be related to the angle θ between the mirrors. The relationship is:
i2=θ−i1
- Substituting this into the total deviation equation gives:
Dtotal=360∘−2(i1+(θ−i1))=360∘−2θ
- We know from the problem statement that the total deviation Dtotal is 240 degrees. Thus, we can set up the equation:
360∘−2θ=240∘
- Rearranging the equation gives:
2θ=360∘−240∘
2θ=120∘
θ=60∘
- The angle between the two mirrors is 60∘.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE-3
Explore 12 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE-04[A]
Explore 23 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE- 01
Explore 45 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
Two plane mirrror are inclined to each other at 70∘. A ray of light is incident on one mirror. They ray after two reflections will undergo a total deviation of :
View SolutionTwo plane mirrors are inclined at 70∘. A ray incident on one mirror at incidence angle θ after reflection falls on the second mirror and is reflected from there parallel to the first mirror, The value of θ is
View SolutionTwo plane mirrors are inclined to each other such that a ray of light incident on the first mirror and parallel to the second is reflected from the second mirror parallel to the first mirror. Determine the angle between the two mirrors:
View SolutionFind the angle between two plane mirrors such that a ray of light incident on the first mirror and parallel to the second mirror is reflected from the second mirror, parallel to the first mirror.
View SolutionTwo plane mirror are inclined to each other at 90∘. A ray of light is incident on one mirror. The ray will undergo a total deviation of
View SolutionA light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,r1,e and the total deviation after two refractions.

View SolutionA ray reflected successively from two plane mirrors inclined at a certain angle (<90∘) undergoes a deviation of 300∘ . The number of images observable are:
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
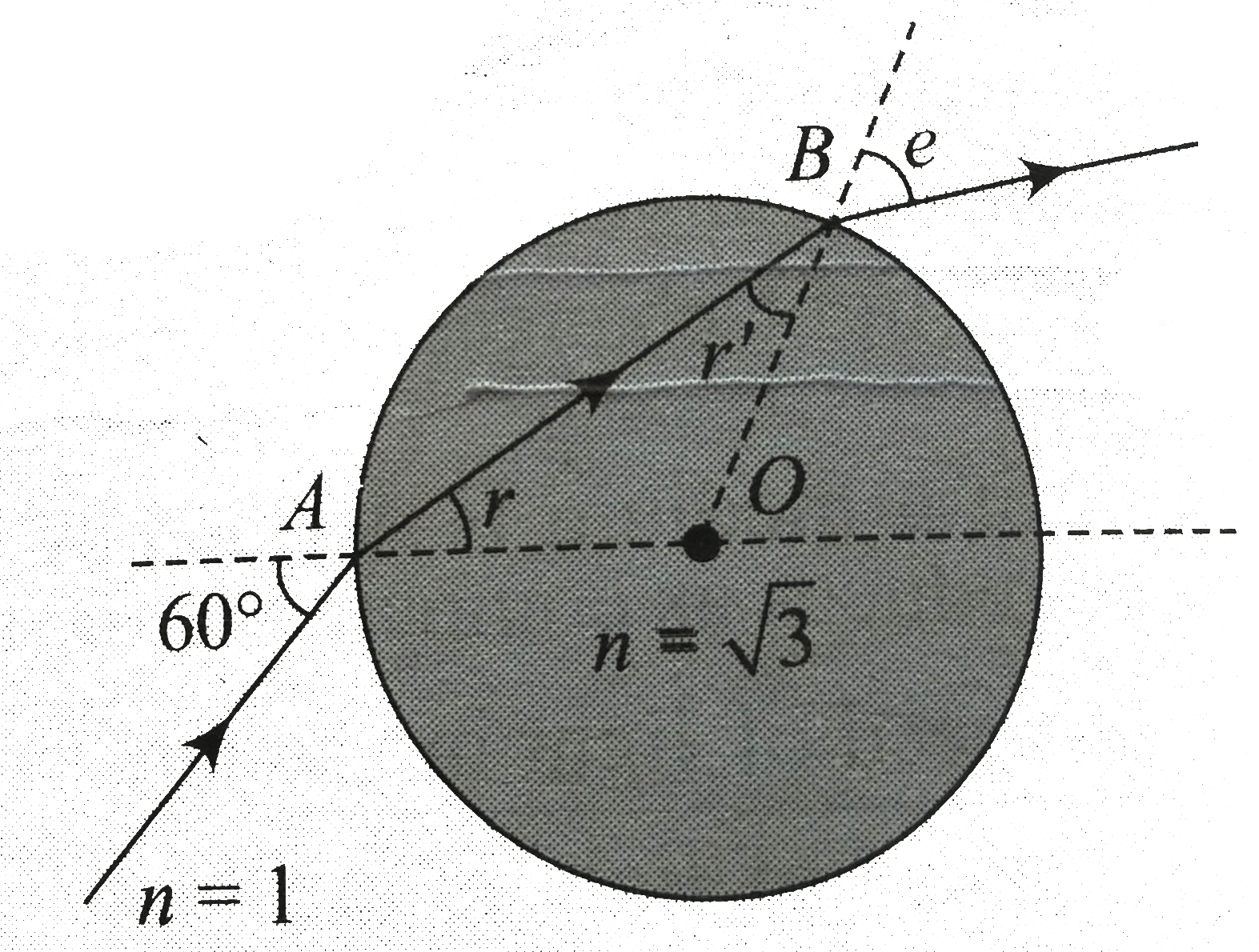
View SolutionTwo plane mirrors are inclined at an angle of 60∘ with each other. An incident ray hits one of the mirror at an angle of 80∘ with the normal. Its angle of deviation after two reflections is
View SolutionTwo plane mirrors are inclined to each other at an angle 60∘ if a ray of light incident on first mirror parallel to the second mirror, it is reflected from the second mirror
View Solution

