Photograph of the ground are taken form an air-craft ,flying at an altitude of 2000 m by a camera with a lens of focal length 50cm. The size of the film in the camera is 18×18cm.What area of the ground can be photography by this camera at any one time.
To find the area of the ground that can be photographed by the camera from an altitude of 2000 m, we will use the concept of linear magnification and the relationship between the area of the image and the area of the object.
1. Identify the Given Values:
- Altitude of the aircraft (h) = 2000 m
- Focal length of the camera lens (f) = 50 cm = 0.5 m
- Size of the film in the camera = 18 cm x 18 cm
2. Calculate the Linear Magnification (m):
The formula for linear magnification (m) in terms of the object distance (u) and the image distance (v) is:
m=vu
Here, we need to find the image distance (v). For a thin lens, the lens formula is:
1f=1v−1u
Rearranging gives:
1v=1f+1u
Given that the object distance (u) is negative (since it is measured in the opposite direction of the incoming light):
u=−2000 m
Substituting the values:
1v=10.5+1−2000
1v=2−0.0005=1.9995
Thus,
v≈11.9995≈0.500125 m
3. Calculate the Linear Magnification (m):
Now substituting the values of v and u into the magnification formula:
m=vu=0.500125−2000≈−0.0002500625
The negative sign indicates that the image is inverted.
4. Calculate the Area of the Image:
The area of the image on the film is given by:
Area of Image=length×width=18 cm×18 cm=324 cm2
5. Calculate the Area of the Object:
The area of the object can be calculated using the formula:
Area of Object=Area of Image×m2
First, calculate m2:
m2≈(0.0002500625)2≈6.25×10−8
Now, substituting back:
Area of Object=324 cm2×1m2=324 cm2×16.25×10−8≈5.184×109 cm2
6. Convert Area to m²:
To convert the area from cm² to m²:
Area of Object≈5.184×109 cm2×(1 m210000 cm2)≈518400 m2
Final Answer:
The area of the ground that can be photographed by this camera at any one time is approximately 518400 m².
- Altitude of the aircraft (h) = 2000 m
- Focal length of the camera lens (f) = 50 cm = 0.5 m
- Size of the film in the camera = 18 cm x 18 cm
The formula for linear magnification (m) in terms of the object distance (u) and the image distance (v) is:
m=vu
Here, we need to find the image distance (v). For a thin lens, the lens formula is:
1f=1v−1u
Rearranging gives:
1v=1f+1u
Given that the object distance (u) is negative (since it is measured in the opposite direction of the incoming light):
u=−2000 m
Substituting the values:
1v=10.5+1−2000
1v=2−0.0005=1.9995
Thus,
v≈11.9995≈0.500125 m
Now substituting the values of v and u into the magnification formula:
m=vu=0.500125−2000≈−0.0002500625
The negative sign indicates that the image is inverted.
The area of the image on the film is given by:
Area of Image=length×width=18 cm×18 cm=324 cm2
The area of the object can be calculated using the formula:
Area of Object=Area of Image×m2
First, calculate m2:
m2≈(0.0002500625)2≈6.25×10−8
Now, substituting back:
Area of Object=324 cm2×1m2=324 cm2×16.25×10−8≈5.184×109 cm2
To convert the area from cm² to m²:
Area of Object≈5.184×109 cm2×(1 m210000 cm2)≈518400 m2
The area of the ground that can be photographed by this camera at any one time is approximately 518400 m².
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
83 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A lens of focal length 12cm forms an upright image three times the size of a real object. Find the distance in cm between the object and image.
View SolutionAn equi-convex lens of focal length F in air is is cut into two halves along the plane perpendicular to the optic axis. One of the halves is placed between a fixed object and a screen separated by distance of 90 cm . Two images are formed on the screen for two different positions of the lens with magnification 2 and 1/2 respectively. Find the value of F . what would be the value of the focal length of the equiconvex lens if the lens is immersed in water ? Refractive index of the material of the lens is 1.5 and that of water is μw=4/3.
View Solution
Knowledge Check
A gaint refrecting telescope at an observatory has an objective lens of focal length 15m. If an eye piece lens of focal length 1cm is used, find the angular magnification of the telescope.
If this telescope is used to view the moon, what is the diameter of image of moon formed by objective lens ? The diameter of the moon is 3.42×106m and radius of lunar orbit is 3.8×108m.A1000B1500C2000D3000A giant telescope in an observatory has an objective of focal length 19 m and an eye-piece of focal length 1.0cm. In normal adjustment, the telescope is used to view the moon. What is the diameter of the image of the moon formed by the objective? The diameter of the moon is 3.5×106m. and the radius of the lunar orbit round the earth is 3.8×108m.
A10cmB12.5cmC15cmD17.5cm
A student focuses the image of a candle flame, placed at about 2 m from a convex lens of focal length 10 cm, on a screen. After that, he moves gradually the flame towards the lens and each time its image on the screen.
(a) In which direction does he move the lens to focus the flame on the screen?
(b) What happens to the size of the image of the flame formed on the screen ?
(c ) What difference is seen in the intensity (brightnees) of the image of the flame on the screen ?
(d) What is seen on the when the flame is very close (at about 5 cm) to the lens ?
View SolutionA point object is located at a distance of 100cm from a screen. A lens of focal length 23 cm mounted on a movable frictionless stad is kept between the source and the screen. The stand is attached to a spring of natureal length 50cm and spring constant 800N/m as shown in Figure . Mass of the stand with lens is 2 kg. How much impulse P should be imparted to the stand so that a real image of the object is formed on the screen after a fixed time gap? Also find this time gap. (Neglect width width of the stand)
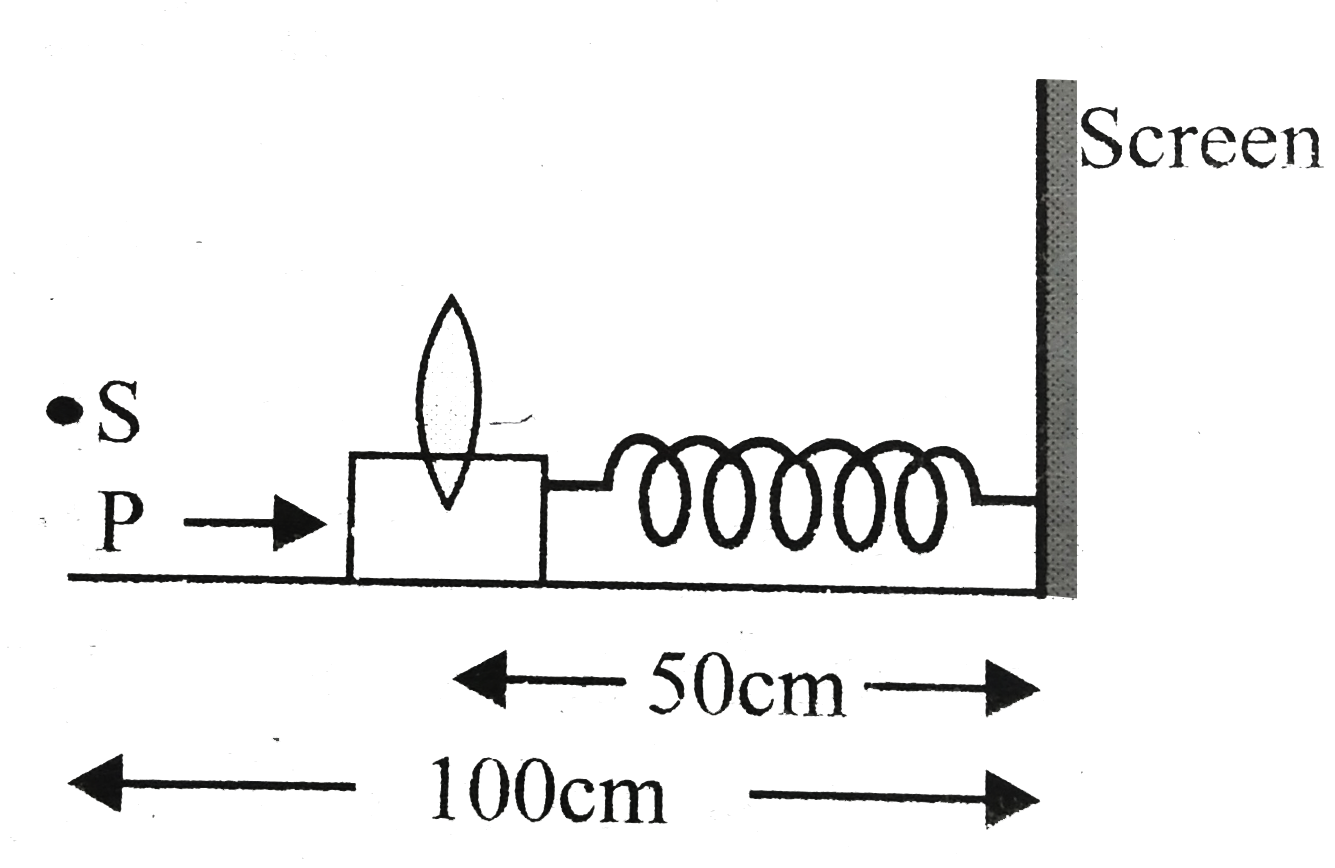
View SolutionA photographic camera with a lens of focal length 5 cm is used for capturing images. The vertical length of the film used is 24 mm in which image of a 1.68 m tall man is to be captured. Find the minimum distance (in m) of the man from the lens such that his complete image can be obtained.
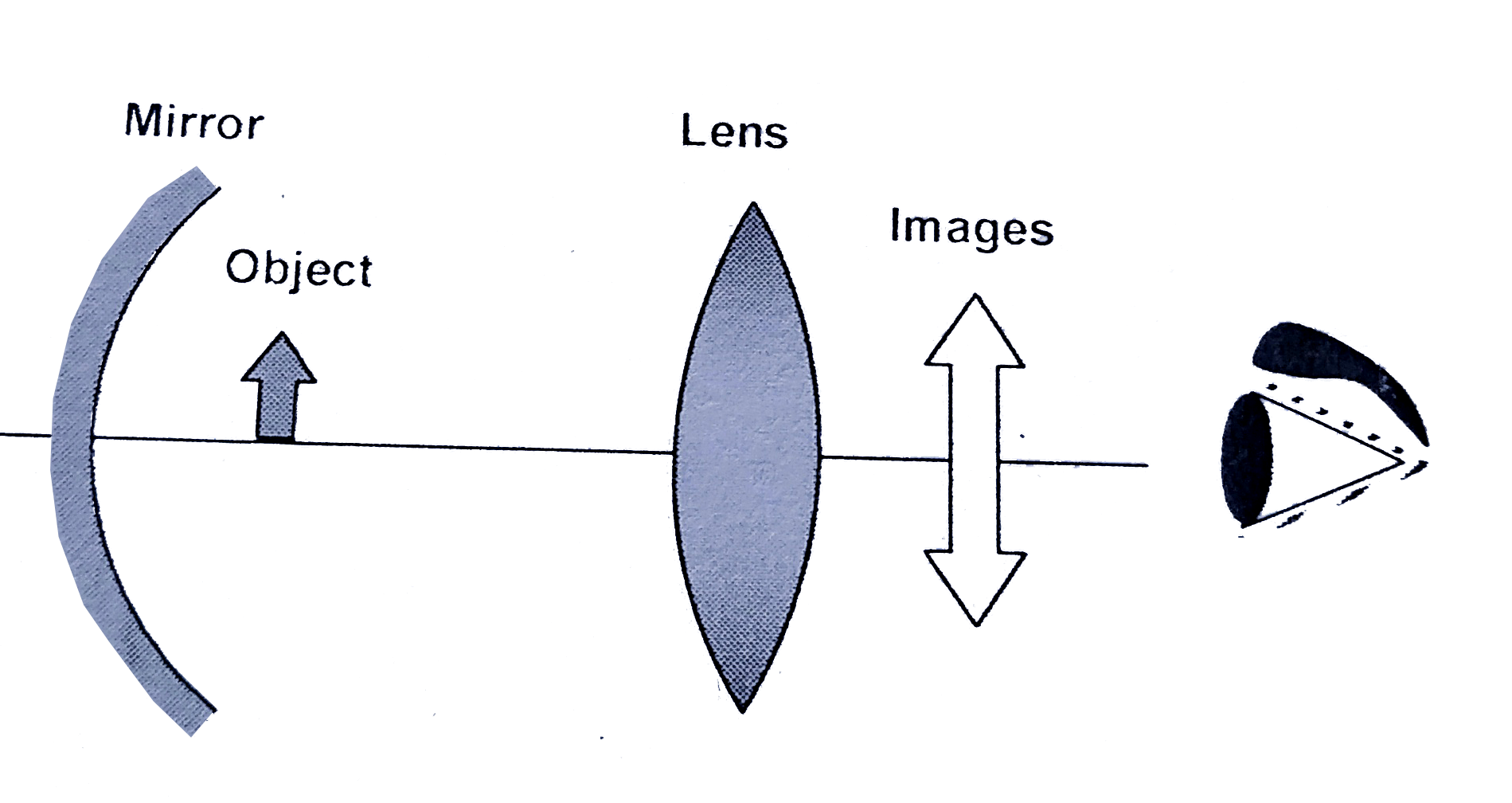
View SolutionAn observer to the right of the mirror-lens combination shown in Figure sees two real images that are the same size and in the same location. One image is upright and the other is inverted. Both images are 1.50 times larger than the object. The lens has a focal length of 10.0cm. The lens and mirror are separated by 40.0cm. Determine the focal length of the mirror. Do not assume that the figure is drawn to scale.
View SolutionOne end of a 60m long rope of mass 1.8 kg is tied to a rigid horizontal support held high above the ground. The rope hangs vertically and kept taut by a weight 'W' suspended at its lower end. A person jerks the lower end of the rope sideways in a sinusoidal manner and a transverse wave of frequency 2 Hz and amplitude 10cm passes along the rope such that there are 2 cycles of the wave in the total length of the rope. Neglecting the weight of the rope as compared to the suspended weight W and with g = 10m/s2, answer the following questions. (S=75×10−4m2)

In the questions above, weight of the rope has been neglected as compared to the suspended weight. However, if we also account for the weight of the rope. the speed of the wave at the top of the rope will be
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart. If a pin of length 2.0 cm is placed 30 cm from the lens farther away from the mirror, where will the final image form and what will be the size of the final image ?
View Solution
