The area of cross-section of rod is given by where & are constant and x is the distance from one end. If the thermal conductivity of the material is . What is the thermal resistancy of the rod if its length is ?
The correct Answer is:B
To find the thermal resistance of the rod with a varying cross-sectional area, we can follow these steps:
1. Understand the Given Information:
- The area of cross-section of the rod is given by:
A=A0(1+αx)
where A0 and α are constants, and x is the distance from one end of the rod.
- The thermal conductivity of the material is given as K.
- The length of the rod is l0.
2. Define Thermal Resistance:
- The thermal resistance R of a rod can be expressed as:
R=LK⋅A
where L is the length of the rod, K is the thermal conductivity, and A is the cross-sectional area.
3. Consider a Differential Element:
- For a small segment dx of the rod, the differential thermal resistance dR can be expressed as:
dR=dxK⋅A(x)
- Substituting the expression for A(x):
dR=dxK⋅A0(1+αx)
4. Integrate to Find Total Resistance:
- To find the total resistance R from x=0 to x=l0, integrate dR:
R=∫l00dxK⋅A0(1+αx)
- Since K and A0 are constants, they can be taken out of the integral:
R=1K⋅A0∫l00dx1+αx
5. Evaluate the Integral:
- The integral ∫dx1+αx can be solved using the natural logarithm:
∫dx1+αx=1αln(1+αx)
- Thus, evaluating from 0 to l0:
R=1K⋅A0(1αln(1+αl0)−1αln(1))
- Since ln(1)=0:
R=1K⋅A0⋅αln(1+αl0)
6. Final Expression for Thermal Resistance:
- Therefore, the thermal resistance of the rod is given by:
R=1K⋅A0⋅αln(1+αl0)
- The area of cross-section of the rod is given by:
A=A0(1+αx)
where A0 and α are constants, and x is the distance from one end of the rod.
- The thermal conductivity of the material is given as K.
- The length of the rod is l0.
- The thermal resistance R of a rod can be expressed as:
R=LK⋅A
where L is the length of the rod, K is the thermal conductivity, and A is the cross-sectional area.
- For a small segment dx of the rod, the differential thermal resistance dR can be expressed as:
dR=dxK⋅A(x)
- Substituting the expression for A(x):
dR=dxK⋅A0(1+αx)
- To find the total resistance R from x=0 to x=l0, integrate dR:
R=∫l00dxK⋅A0(1+αx)
- Since K and A0 are constants, they can be taken out of the integral:
R=1K⋅A0∫l00dx1+αx
- The integral ∫dx1+αx can be solved using the natural logarithm:
∫dx1+αx=1αln(1+αx)
- Thus, evaluating from 0 to l0:
R=1K⋅A0(1αln(1+αl0)−1αln(1))
- Since ln(1)=0:
R=1K⋅A0⋅αln(1+αl0)
- Therefore, the thermal resistance of the rod is given by:
R=1K⋅A0⋅αln(1+αl0)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -02
Explore 82 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -03
Explore 10 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:SOME WORKED OUT EXAMPLES
Explore 83 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
One end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
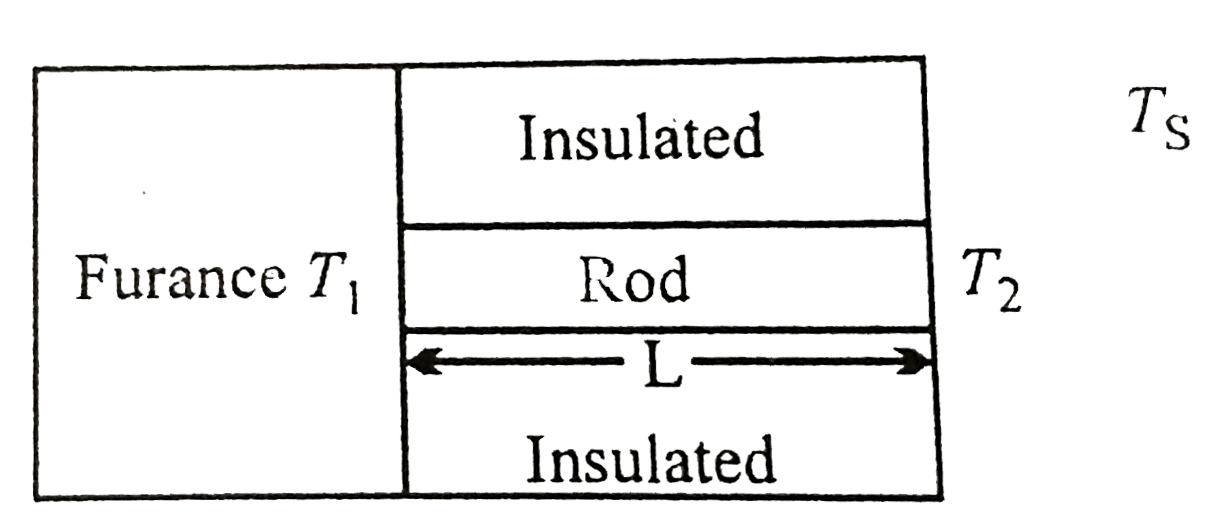
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View Solution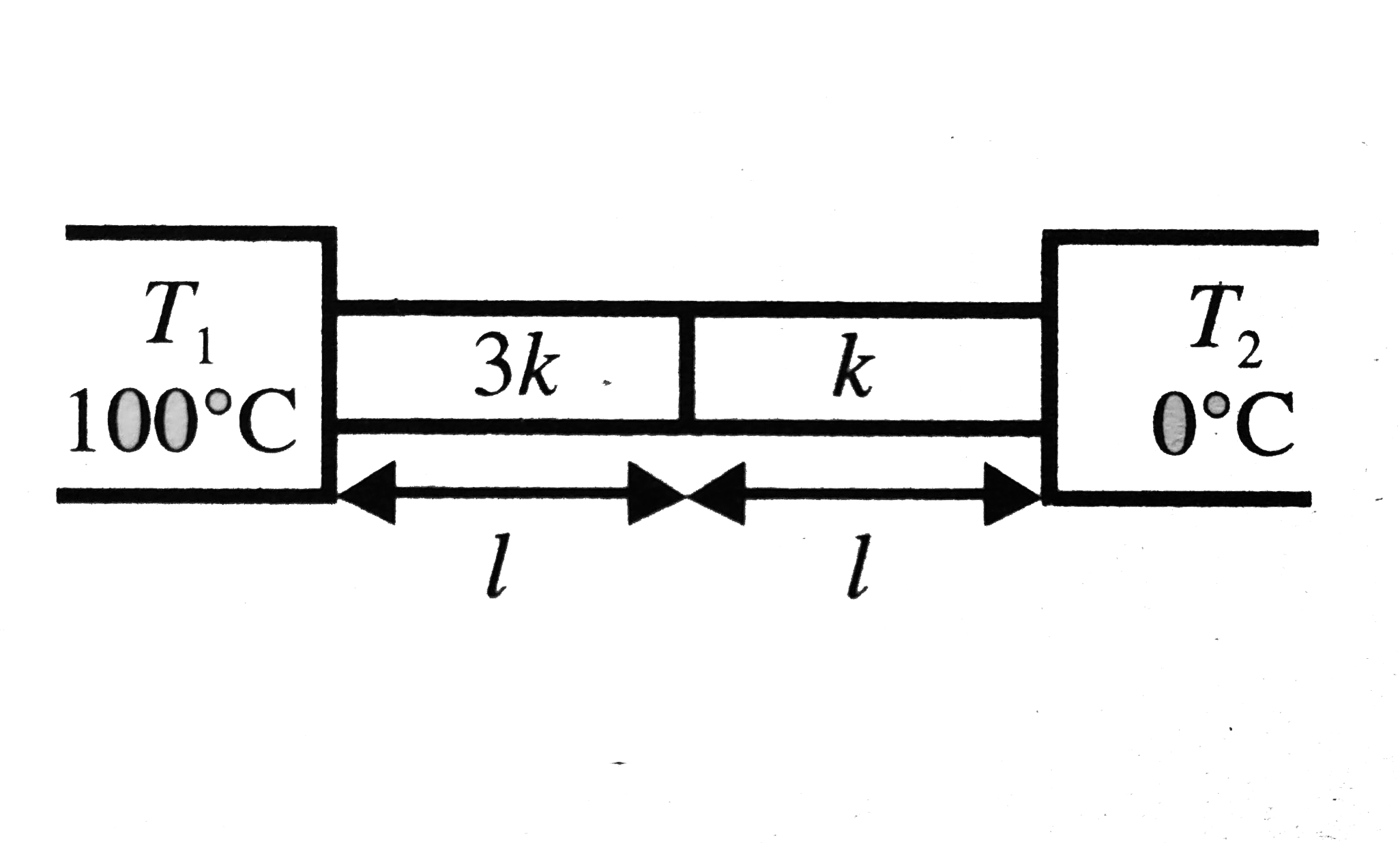
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1) . Thermal conductivity of the material of the rod is K.

View SolutionA cylindrical rod with one end in a steam chamber and the other end in ice results in melting of 0.1 g of ice per second. If the rod is replaced by another with half the length and double the radius of the first and if the thermal conductivity of material of second rod is 1/4 that of first, the rate at which ice melts in g/s will be
View SolutionA cylindrical block of length 0.4 m and area of cross-section 0.04m2 is placed coaxially on a thin metal disc of mass 0.4 kg and of the same cross - section. The upper face of the cylinder is maintained at a constant temperature of 400 K and the initial temperature of the disc is 300K. if the thermal conductivity of the material of the cylinder is 10watt/m−K and the specific heat of the material of the disc is 600J/kg−K, how long will it take for the temperature of the disc to increase to 350 K? Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder.
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionThe displacement of a particle is given by
x=a0+a1t3−a2t22
where a0,a1 and a2 are constants. What is its acceleration ?
View SolutionA copper rod 2 m long has a circular cross-section of radius 1 cm. One end is kept at 100∘C and the other at 0∘C. The surface is insulated so that negligible heat is lost through the surface. In steady state, find
(a) the thermal resistance of the bar
(b) the thermal current H
(c) the temperature gradient dTdx and
(d) the temperature at a distance 25 cm from the hot end.
Thermal conductivity of copper is 401 W/m−K.
View SolutionA copper rod 2 m long has a circular cross-section of radius 1 cm. One end is kept at 100∘C and the other at 0∘C. The surface is insulated so that negligible heat is lost through the surface. In steady state, find
(a) the thermal resistance of the bar
(b) the thermal current H
(c) the temperature gradient dTdx and
(d) the temperature at a distance 25 cm from the hot end.
Thermal conductivity of copper is 401 W/m.K.
View Solution