Two absolute scales X and Y assigned numerical values 200 and 450 to the triple of water. What is the relation between TX and TY ?
9TX=4TY
4TX=9TY
TX=3TY
None of these
The correct Answer is:A
To find the relation between the temperatures TX and TY assigned to the triple point of water on two different absolute scales X and Y, we can follow these steps:
1. Understand the given values:
- The triple point of water is assigned a value of 200 on scale X and 450 on scale Y.
- We denote the triple point of water in Kelvin as TK=273.15K.
2. Set up the equations:
- From the problem, we can express the temperatures on the scales as:
TX=200(scale X)
TY=450(scale Y)
3. Relate the scales to Kelvin:
- Since the triple point of water is the same physical temperature, we can relate the two scales to Kelvin:
TX=kX⋅200
TY=kY⋅450
- Here, kX and kY are the conversion factors from scales X and Y to Kelvin.
4. Find the conversion factors:
- We know that at the triple point of water:
TX=TK⟹kX⋅200=273.15⟹kX=273.15200
TY=TK⟹kY⋅450=273.15⟹kY=273.15450
5. Relate TX and TY:
- Now we can express TX and TY in terms of TK:
TX=273.15200⋅200=273.15
TY=273.15450⋅450=273.15
- Since both equal TK, we can set up the ratio:
TXTY=273.15200⋅200273.15450⋅450=450200
6. Simplify the ratio:
- Simplifying the ratio gives:
TXTY=450200=94
- Therefore, we can express this relationship as:
9TX=4TY
Final Relation:
Thus, the relation between TX and TY is:
9TX=4TY
- The triple point of water is assigned a value of 200 on scale X and 450 on scale Y.
- We denote the triple point of water in Kelvin as TK=273.15K.
- From the problem, we can express the temperatures on the scales as:
TX=200(scale X)
TY=450(scale Y)
- Since the triple point of water is the same physical temperature, we can relate the two scales to Kelvin:
TX=kX⋅200
TY=kY⋅450
- Here, kX and kY are the conversion factors from scales X and Y to Kelvin.
- We know that at the triple point of water:
TX=TK⟹kX⋅200=273.15⟹kX=273.15200
TY=TK⟹kY⋅450=273.15⟹kY=273.15450
- Now we can express TX and TY in terms of TK:
TX=273.15200⋅200=273.15
TY=273.15450⋅450=273.15
- Since both equal TK, we can set up the ratio:
TXTY=273.15200⋅200273.15450⋅450=450200
- Simplifying the ratio gives:
TXTY=450200=94
- Therefore, we can express this relationship as:
9TX=4TY
Thus, the relation between TX and TY is:
9TX=4TY
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -02
Explore 82 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -03
Explore 10 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:SOME WORKED OUT EXAMPLES
Explore 83 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
Two absolute scales A and B have triple points of water defined to be 200A and 350B. What is the relation between TA and TB?
View SolutionIn the show indicator diagram over pressure - volume scales 'n' moles of an ideal gas is cycled . If the temperature of the gas in the state X and Y are respectively TXandTY . Temperature of the gas in the state Z is the (All temperature are in absolute scale )
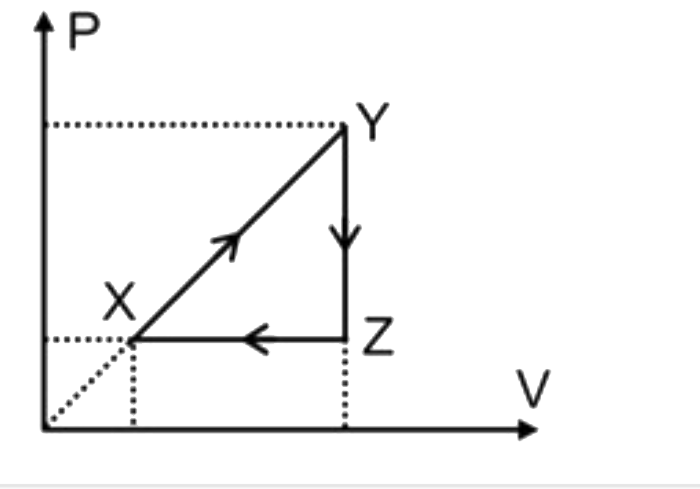
View Solution
Knowledge Check

Relation between (X) and (Y) is :AenantiomersBdiastereomersCE and Z isomerDconstitutional isomerTwo absolute scales A and B have triple points of water defined to be 200A and 350B. What is the relation between TA and TB?
ATA=4/7TBBTB=4/7TACTA=2/7TBDTB=2/7TAIf the parameter is eliminated from the equations x=t2+1andy=2t, then the relation between x and y is
Ay=x−1By=1−xCy2=x−1Dy2=4x−4
In a termperature scale X ice point of water is assigned a value of 20∘X and the boiling point of water is assiggned a value of 220∘X. In another scale Y the ice poiny of water is assigned a value of −20∘Y and the boiling point is given a value of 380∘Y. Then temperature on both the scales will be same is
View SolutionOn the absolute scale triple point of water is one fixed temperature, what is the other?
View SolutionA curve is represented parametrically by the equations x=etcostandy=etsint where t is a parameter. Then The relation between the parameter 't' and the angle a between the tangent to the given curve andthe x-axis is given by, 't' equals
View SolutionAbsolute refractive index of a medium is X. Refractive index of same medium w.r.t to air is Y and absolute refractive index to air is Z. Then the relation between them is
View SolutionTwo sinusoidal waves in a string are defined by the function y1=(2.00cm)sin(20.0x−32.0t) and y2=(2.00cm)sin(25.0x−40.0t) where y1,y2 and x are in centimetres and t is in seconds.
(a). What is the phase difference between these two waves at the point x=5.00cm at t=2.00s?
(b) what is the positive x value closest to the original for which the two phase differ by +πatt=2.00s? (That os a location where the two waves add to zero.)
View Solution