A meter washer has a hole of diameter d1 and external diameter d2, where d2=3d1. On heating , d2 increases by 0.3%. Then d1 will :-
decreases by 0.1%
decrease by 0.3%
increases by 0.1%
increase by 0.3%.
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the diameters of the washer and how they change with temperature.
1. Understand the relationship between diameters:
Given that the external diameter d2 is three times the internal diameter d1:
d2=3d1
2. Determine the percentage increase in d2:
It is given that d2 increases by 0.3%. We can express this mathematically:
Δd2=0.003⋅d2
3. Calculate the new value of d2:
The new diameter d′2 after heating can be calculated as:
d′2=d2+Δd2=d2+0.003⋅d2=d2(1+0.003)=1.003d2
4. Relate the change in d2 to d1:
Since both diameters expand due to heating, we can express the change in d1 similarly. Let Δd1 be the change in d1:
Δd1=0.003⋅d1
Thus, the new diameter d′1 will be:
d′1=d1+Δd1=d1+0.003⋅d1=d1(1+0.003)=1.003d1
5. Express the new d′2 in terms of d′1:
Since d′2=3d′1, we can substitute d′1:
d′2=3(1.003d1)=3.009d1
6. Set up the equation:
We know from the earlier step that d′2=1.003d2 and substituting d2=3d1:
1.003(3d1)=3.009d1
This confirms our relationship holds true.
7. Conclusion:
Since both diameters increase by the same percentage, we can conclude that the internal diameter d1 also increases by 0.3%.
Final Answer:
Thus, the internal diameter d1 will also increase by 0.3%.
Given that the external diameter d2 is three times the internal diameter d1:
d2=3d1
It is given that d2 increases by 0.3%. We can express this mathematically:
Δd2=0.003⋅d2
The new diameter d′2 after heating can be calculated as:
d′2=d2+Δd2=d2+0.003⋅d2=d2(1+0.003)=1.003d2
Since both diameters expand due to heating, we can express the change in d1 similarly. Let Δd1 be the change in d1:
Δd1=0.003⋅d1
Thus, the new diameter d′1 will be:
d′1=d1+Δd1=d1+0.003⋅d1=d1(1+0.003)=1.003d1
Since d′2=3d′1, we can substitute d′1:
d′2=3(1.003d1)=3.009d1
We know from the earlier step that d′2=1.003d2 and substituting d2=3d1:
1.003(3d1)=3.009d1
This confirms our relationship holds true.
Since both diameters increase by the same percentage, we can conclude that the internal diameter d1 also increases by 0.3%.
Thus, the internal diameter d1 will also increase by 0.3%.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
10 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
83 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Two holes of unequal diameters d1 and d2(d1>d2) are cut in metal sheet is heated
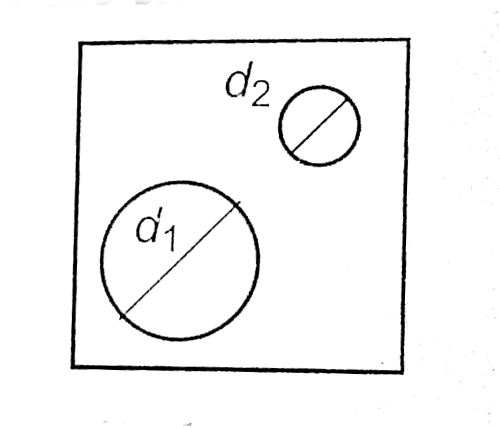
View SolutionTwo holes of unequal diameters d1andd2 (d1>d2)d2 are cut in metal sheet. If the sheet is heated

View SolutionIn Young's double slit experiment the 7th maximum with wavelength λ1is at a distance d1, and that with wavelength λ2 is at distance d2. Then d1/d2 is
View SolutionIf equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View SolutionThe ratio of the area and circumference of a circle of diameter d is
(a)d
(b) d2
(c)d4
(d) 2 d
View SolutionRadiation from a black body at the thermodynamic temperature T1 is measured by a small detector at distance d1 from it. When the temperature is increased to T2 and the distance to d2 , the power received by the detector is unchanged. What is the ratio d2/d1?
View SolutionThe distance between two points P and Q is d and the length of their projections of PQ on the co-ordinate planes are d1,d2,d3. Then d21+d22+d23=kd2, where k is _____.
View SolutionThe distance between two points P and Q is d and the length of their projections of PQ on the co-ordinate planes are d1,d2,d3. Then d21+d22+d23=kd2, where k is _____.
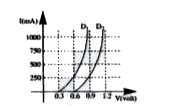
View SolutionThe forward bias characteristics of two diodes D1andD2 are shown, the knee voltage for D1andD2 are respectively (approx)
View SolutionA camera objective has an aperture diameter d . If the aperture is reduced to diameter d/2 the exposure time under identical conditions of light should be made
View Solution