The figure shows the cross-section of the outer wall of a house buit in a hill-resort to keep the house insulated from the freezing temperature of outside. The wall consists of teak wood of thickness L1 and brick of thickness (L2=5L1), sandwitching two layers of an unknown material with identical thermal conductivites and thickness. The thermal conductivity of teak wood is K1 and that of brick is (K2=5K1). Heat conducion through the wall has reached a steady state with the temperature of three surfaces being known. (T1=25∘C,T2=20∘C and T5=−20∘C). Find the interface temperature T4 and T3.

Let interface area be A. Then thermal resistance of wood,R1=L1K1A and that of brick wall R2=L2K2A=5L15K1A=R1
Let thermal resistance of the each sand witch layer= R. Then the above wall can be visualised as a circuit
Thermal current through each wall is same.
Hence 25−20R1=20−T2R=T3−T4R=T4+20R1
⇒25−20=T4+24⇒T4=−15∘C
also, 20−T3=T3−T4⇒T3=20+T42=2.5∘C
(##ALN_PHY_C07(I)_S01_011_S01.png" width="80%">
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
83 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View Solution
Knowledge Check
Consider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
A23KB√2KC3KD43KTwo walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
AK1T1d2+K2T2d1K1d2+K2d1BK1T1+K2T2d2+d1C(K1d1+K2d2T1+T2)T1T2DK1T1d1+K2T2d2K1d1+K2d2A wall has two layers A and B, each made of different material. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B . Under thermal equilibrium, the temperature difference across the wall is 36∘C. The temperature difference across the layer A is
A12.∘CB18.∘CC6.∘CD24.∘C
The thermal conductivity of brick is 1.7Wm−1K−1, and that of cement is 2.9Wm−1K−1.What thickness of cement will have same insulation as the brick of thickness 20cm.
View SolutionA composite slab is made of two parallel layers of two different materials of thermal conductivities K1andK2 are of same thickness. Show that the equivalent thermal conductivity of the slab is 2K1K2K1+K2
View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionThe wall of a house is made of two different materials of same thickness. The temperatures of the outer wall is T2 and that of inner wall is T1<T2. The temperature variation inside the wall as shown in the figure. Then :
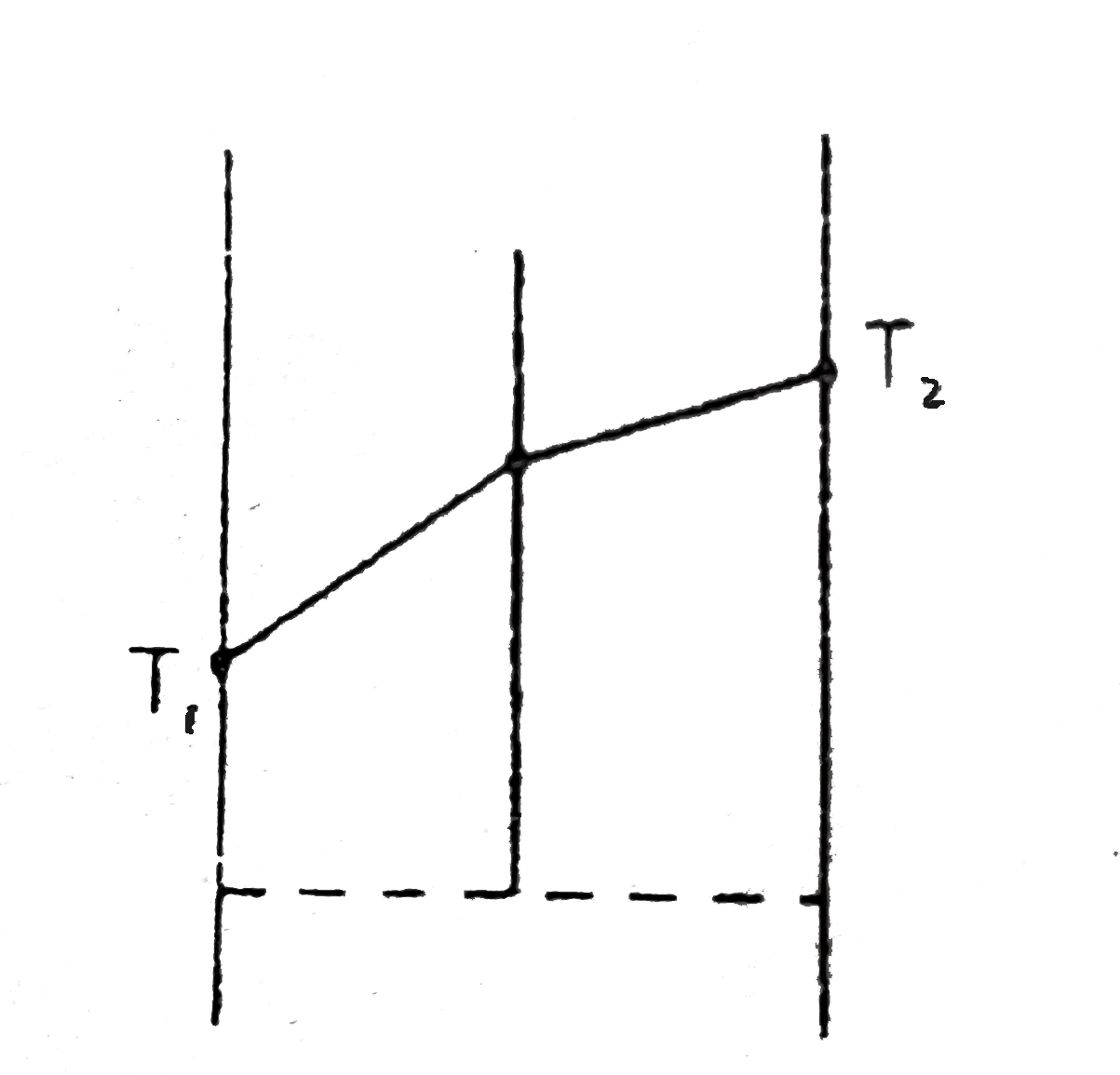
View SolutionA wall has two layers A and B, each made of different material. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B . Under thermal equilibrium, the temperature difference across the wall is 36∘C. The temperature difference across the layer A is
View Solution
