A particle is moving under the influence of a force which is fixed in magnitude and acting at an angle θ in the direction of motion. The path described by the particle is
a circle
an ellipse
a parabola
a straight line
The correct Answer is:C
To solve the problem, we need to analyze the motion of a particle under the influence of a force that is fixed in magnitude and acts at an angle θ to the direction of motion.
1. Understanding the Force and Motion:
The particle is moving in a certain direction with a velocity →v. A force →F is applied at an angle θ to the direction of this motion.
2. Components of the Force:
The force can be broken down into two components:
- A component along the direction of motion: F∥=Fcos(θ)
- A component perpendicular to the direction of motion: F_{\perpendicular} = F \sin(\theta)
3. Effect of the Force:
The component F∥ will cause the particle to accelerate in the direction of motion, while F_{\perpendicular} will change the direction of the velocity of the particle.
4. Acceleration Calculation:
According to Newton's second law, the acceleration →a of the particle can be calculated using:
→a=→Fm
where m is the mass of the particle. The acceleration will have both a tangential component (due to F∥) and a normal component (due to F_{\perpendicular} ).
5. Path of the Particle:
The presence of a force at an angle θ means that the particle will not move in a straight line. Instead, the combination of the tangential acceleration (which increases the speed) and the normal acceleration (which changes the direction) will result in a curved path.
6. Identifying the Path Shape:
The path described by the particle under these conditions is similar to that of a projectile motion, which is a parabolic trajectory. This is because the particle is subjected to a constant acceleration in the direction of the force while also changing direction.
7. Conclusion:
Therefore, the path described by the particle is a parabola.
Final Answer:
The path described by the particle is a parabola.
---
The particle is moving in a certain direction with a velocity →v. A force →F is applied at an angle θ to the direction of this motion.
The force can be broken down into two components:
- A component along the direction of motion: F∥=Fcos(θ)
- A component perpendicular to the direction of motion: F_{\perpendicular} = F \sin(\theta)
The component F∥ will cause the particle to accelerate in the direction of motion, while F_{\perpendicular} will change the direction of the velocity of the particle.
According to Newton's second law, the acceleration →a of the particle can be calculated using:
→a=→Fm
where m is the mass of the particle. The acceleration will have both a tangential component (due to F∥) and a normal component (due to F_{\perpendicular} ).
The presence of a force at an angle θ means that the particle will not move in a straight line. Instead, the combination of the tangential acceleration (which increases the speed) and the normal acceleration (which changes the direction) will result in a curved path.
The path described by the particle under these conditions is similar to that of a projectile motion, which is a parabolic trajectory. This is because the particle is subjected to a constant acceleration in the direction of the force while also changing direction.
Therefore, the path described by the particle is a parabola.
The path described by the particle is a parabola.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:SWOE
Explore 44 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
In brownian motion , the paths of the particles are :
View SolutionA particle moves in x-y plane in figure under the influence of a friction force with magnitude 3.00N and acting in the direction opposite to the particle's displacement. Calculate the work done by the friction force on particle as it moves along the following paths: (a) path OA followed by AC (b) path OA followed by AC and the return path CO, (c) path OC followed by the return path CO, and (d) each of your three answers should be non-zero. What is the significant of this observation?

View Solution
Knowledge Check
A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
Astraight lineBarc of circleCparabolaDellipse
A particle at rest on a frictionless table is acted upon by a horizontal force which is constant in magnitude and direction. A graph is plotted of the work done on the particle W, against the speed of the particle v. If there are no frictional forces acting on the particle, the graph will look like
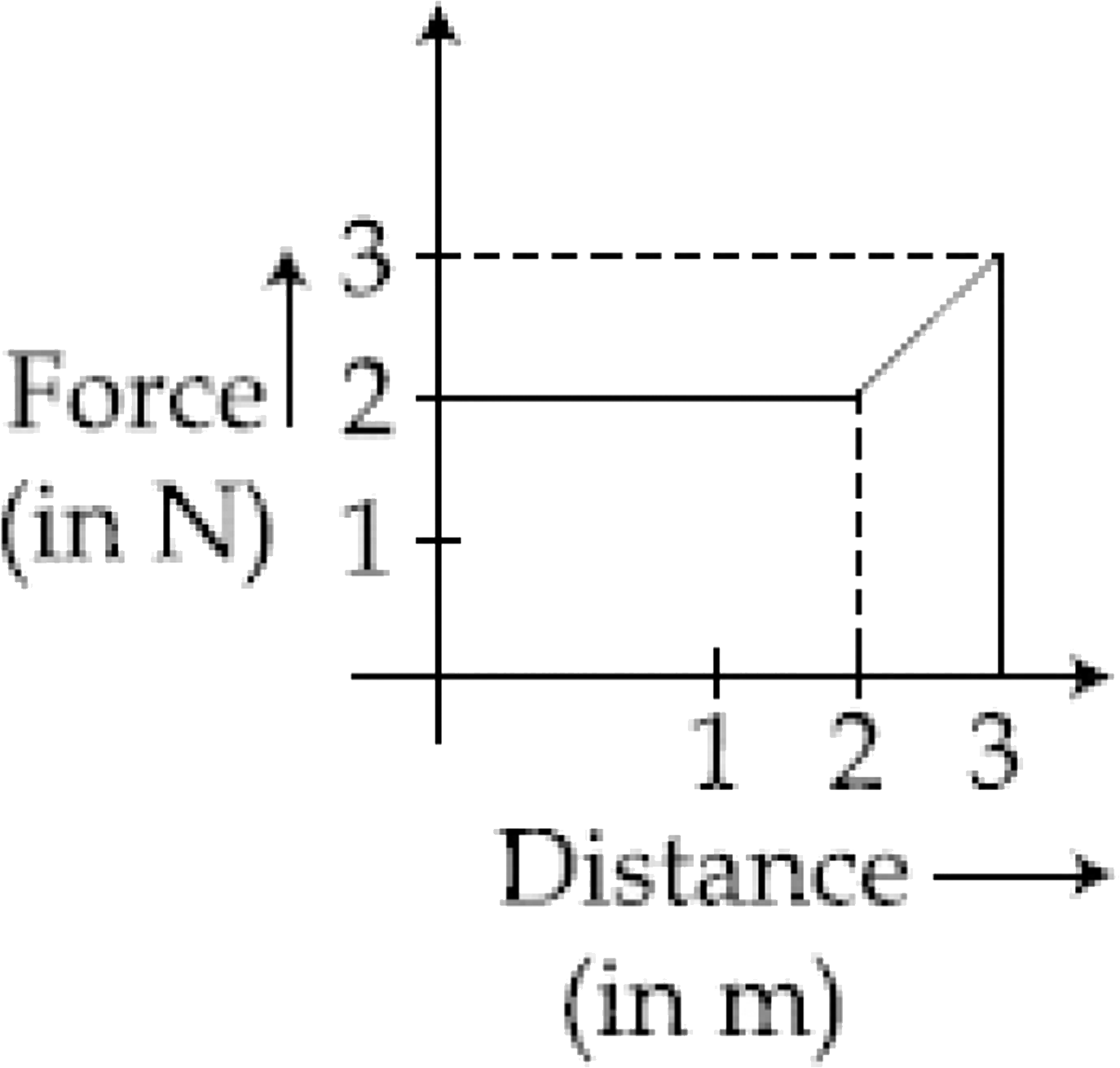
View SolutionA particle moves in one dimension from rest under the influence of a force that varies with the distance travelled by the particle as shown in the figure. The kinetic energy of the particle after it has travelled 3m is:
View SolutionA particle moving along a circular path due to a centripetal force having constant magnitude is an example of motion with :
View SolutionA particle of mass 120 g moving at speed of 750 cm/s is acted upon by a variable force opposite to its direction of motion. If the velocity of the particle becomes 250 cm/s along the direction of force, find the value of time 't' for which acted.
View SolutionA particle of mass m starts moving from origin along a horizontal x-y plane under the influence of a force of constant magnitude F ( which is always parallel to the x-axis ) and a constraint force. The trajectory of its motion is f(x)=xx2+1. Then,
View SolutionA particle moving with a velocity equal to 0.4ms−1 is subjected to an acceleration of 0.15ms−2 for 2 seconds in a direction at right angles to the direction of motion. The magnitude of the final velocity is
View SolutionWhen a force of constant magnitude in a fixed direction acts on a moving object, then its path is -
View Solution
