A cyclist on the ground goes round a ciruclar path of circumference 34.3 m in √22 second. The angle made by him, with the vertical, will be:-
45∘
40∘
42∘
48∘
The correct Answer is:A
To solve the problem, we need to determine the angle made by the cyclist with the vertical while moving in a circular path. Here’s a step-by-step breakdown of the solution:
Step 1: Calculate the Radius of the Circular Path
We know the circumference C of the circular path is given as 34.3m. The formula for the circumference of a circle is:
C=2πr
From this, we can solve for the radius r:
r=C2π=34.32π
Step 2: Calculate the Velocity of the Cyclist
The time taken to complete the circular path is given as √22s. The velocity V can be calculated using the formula:
V=DistanceTime=34.3√22m/s
Step 3: Use the Formula for the Angle with the Vertical
In circular motion, the angle θ made with the vertical can be calculated using the formula:
tanθ=V2rg
where g is the acceleration due to gravity (approximately 10m/s2).
Step 4: Substitute the Values
First, we need to calculate V2:
V2=(34.3√22)2=34.3222
Now, substituting r and g into the formula:
tanθ=34.3222(34.32π)⋅10
Step 5: Simplify the Expression
Substituting r:
tanθ=34.3222⋅2π34.3⋅10
This simplifies to:
tanθ=34.320π
Step 6: Calculate the Angle
To find θ, we can use the arctangent function:
θ=tan−1(34.320π)
Calculating this gives us an approximate value for θ.
Step 7: Final Answer
The angle made by the cyclist with the vertical is approximately 45∘.
We know the circumference C of the circular path is given as 34.3m. The formula for the circumference of a circle is:
C=2πr
From this, we can solve for the radius r:
r=C2π=34.32π
The time taken to complete the circular path is given as √22s. The velocity V can be calculated using the formula:
V=DistanceTime=34.3√22m/s
In circular motion, the angle θ made with the vertical can be calculated using the formula:
tanθ=V2rg
where g is the acceleration due to gravity (approximately 10m/s2).
First, we need to calculate V2:
V2=(34.3√22)2=34.3222
Now, substituting r and g into the formula:
tanθ=34.3222(34.32π)⋅10
Substituting r:
tanθ=34.3222⋅2π34.3⋅10
This simplifies to:
tanθ=34.320π
To find θ, we can use the arctangent function:
θ=tan−1(34.320π)
Calculating this gives us an approximate value for θ.
The angle made by the cyclist with the vertical is approximately 45∘.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:SWOE
Explore 44 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
A cyclist goes around a circular track of circumference 410 m in 20 s. Find the angle that his cycle makes with the vertical.
View SolutionA cyclist riding at a speed, of 24.25ms−1 takes a round a circular road of radius 34.64 m. What is his inclination to the vertical ?
View SolutionFig. show a conical pendulum. If the length of the pendulum is l, mass of die bob is m and θ is the angle made by the string with the vertical show that the angular momentum of the pendulum about the point of support is:
L=√m2gl3sin4θcosθ
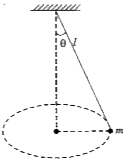
View SolutionA cyclist moves around a circular path of radius 39.2√3 metre with a speed of 19.6ms−1 '. He must lean inwards at an angle θ with the vertical such that tanθ is
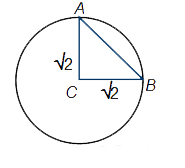
View SolutionA man starts running with constant speed along a circular path of radius √2m He completes two rounds in 16 seconds. The magnitude of the average velocity in first 2 seconds is
View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
View SolutionA uniform rod of length l and mass m is suspended from one end by inextensible string and other end less lies on smooth ground. The angle made by the rod with vertical is θ=sin−1(1/√3). If N1 and N2 represent the contact force from ground on rod just before and just after cutting the string then the ratio of N1/N2 is 0.25 x. Find the value of x.

View SolutionA simple pendulum having a bob of mass m under goes small oscillations with amplitude θ0 Find the tension in the string as a function of the angle made by the string with the vertical. When in this tension maximum, and when is it minimum?
View SolutionA cyclist rides round a curved path of radius 10m at a speed 18 kmph. If the cycle and the rider together have a mass of 100 kg, the firctional force the ground exerts on the wheel is (g = 10 ms2)
View SolutionA circus artist is climbing a 30 m rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole to the ground. Find the height of the angle made by the rope with the ground level is 30∘), as shown in the figure.

View Solution

