Question

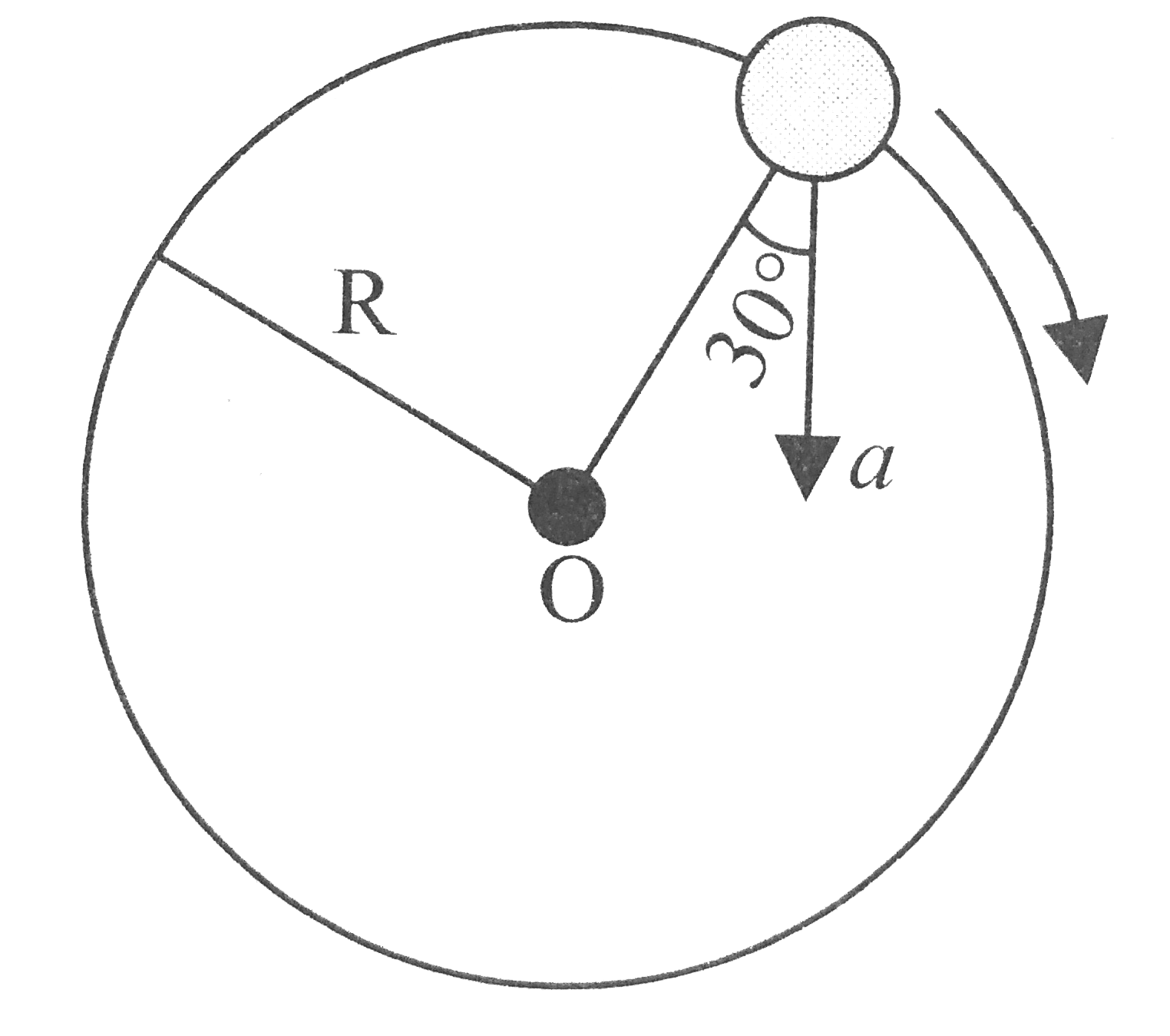
Figure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius $2.5m$ at a given instant of time. At this instant, find:
(a) the radial acceleration,
(b) the speed of the particle,
(c) its tangential acceleration.

Answer

(i) `25 sqrt(3)/2 m//s^(2)` (ii) `(125sqrt(3)/4)^(1//2) m//s` (iii) `25/2 m//s^(2)`

Explanation

`r=2.5 m, a_("net")=25 m//s^(2)`
(a) Radial acceleration `=25 cos theta=25xxsqrt(3)/3 m//s^(2)`
(b) `25 sqrt(3)/2=v^(2)/25rArr v=(125 sqrt(3)/4)^(1//2) m//s`
(c) Tangential acceleration `=25 sin theta=25xx1/2 m//s^(2)`