The angular velocity of a particle moving in a circle of radius 50cm is increased in 5 min from 100 revolutions per minute to 400 revolutions per minute. Find the tangential acceleration of the particle.
60ms−2
π/30ms−2
π/15ms−2
π/60ms−2
The correct Answer is:D
To solve the problem step by step, we will follow the given information and apply the necessary formulas.
Step 1: Convert initial and final angular velocities to radians per second
The initial angular velocity (ωi) is given as 100 revolutions per minute (rpm). To convert this to radians per second, we use the conversion factor 2π radians per revolution and divide by 60 seconds per minute.
ωi=100rev/min×2πrad1rev×1min60s=100×2π60=100π30=10π3rad/s
The final angular velocity (ωf) is given as 400 revolutions per minute. We convert this similarly:
ωf=400rev/min×2πrad1rev×1min60s=400×2π60=400π30=40π3rad/s
Step 2: Calculate the angular acceleration (α)
The angular acceleration can be found using the formula:
ωf=ωi+αt
We know that the time t is 5 minutes, which we convert to seconds:
t=5min×60s/min=300s
Now substituting the values into the equation:
40π3=10π3+α×300
Rearranging gives:
α×300=40π3−10π3=30π3=10π
Now, solving for α:
α=10π300=π30rad/s2
Step 3: Calculate the tangential acceleration (at)
The tangential acceleration can be calculated using the formula:
at=rα
Where r is the radius. The radius is given as 50 cm, which we convert to meters:
r=50cm=0.5m
Now substituting the values:
at=0.5m×π30rad/s2=0.5π30=π60m/s2
Final Answer
The tangential acceleration of the particle is:
π60m/s2
The initial angular velocity (ωi) is given as 100 revolutions per minute (rpm). To convert this to radians per second, we use the conversion factor 2π radians per revolution and divide by 60 seconds per minute.
The angular acceleration can be found using the formula:
The tangential acceleration can be calculated using the formula:
The tangential acceleration of the particle is:
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Multiple Correct
Explore 11 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Assertion - Reasoning
Explore 5 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Subjective
Explore 40 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A particle moves in a circle of radius 20 cm. Its linear speed is given by v=2t, where t is in second and v in metre/ second. Find the radial and tangential acceleration at t=3s.
View SolutionA particle moves in a circle of radius 30cm. Its linear speed is given by v=2t, where t in second and v in m/s. Find out its radial and tangential acceleration at t=3s.
View SolutionFigur shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5m at a given instant of time. At this instant, find:
(a) the radius acceleration,
(b) the speed of the acceleration,
(c) its tangential acceleration.
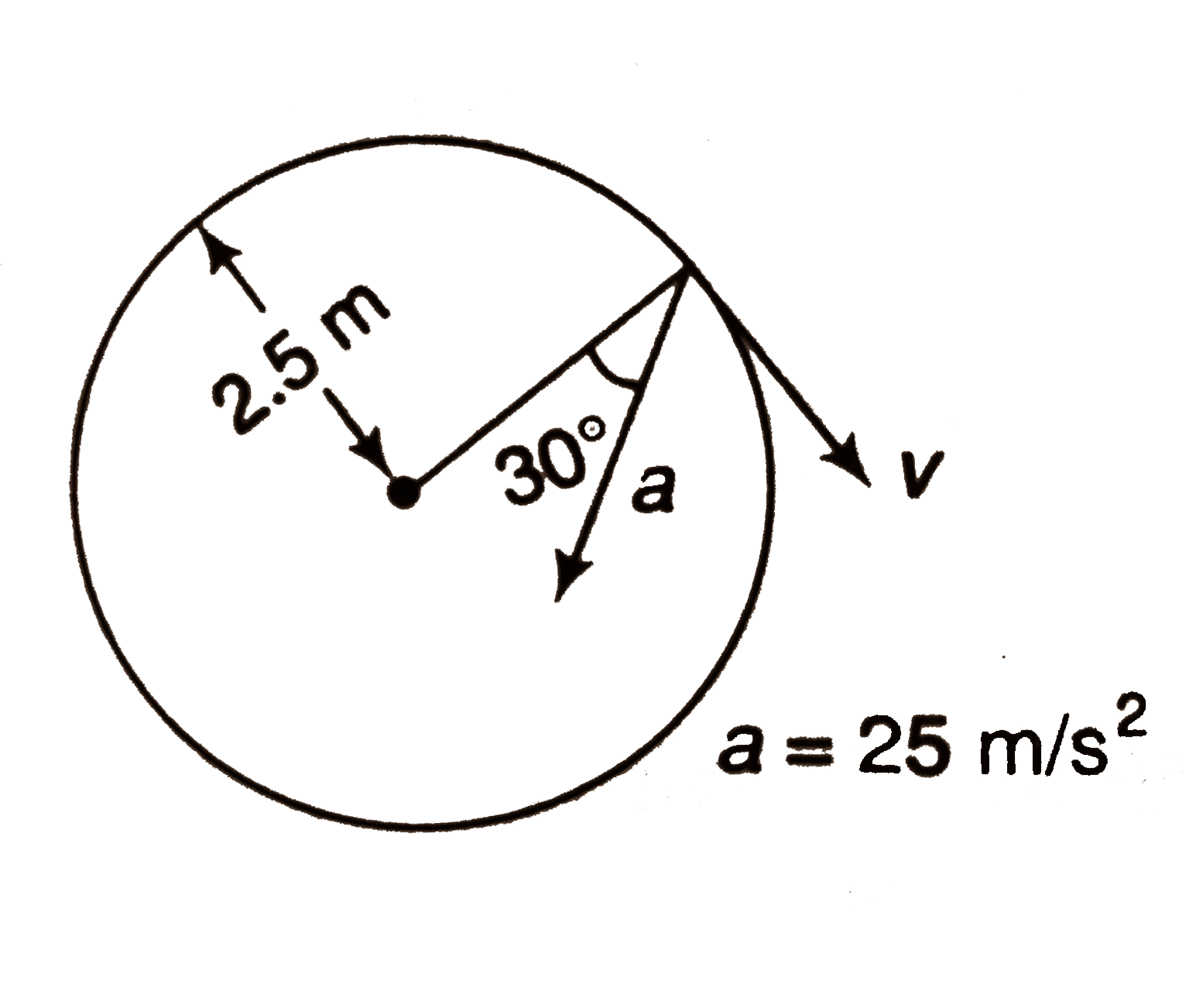
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View SolutionFind the magnitude of the linear acceleration of a particle moving in a circle of radius 10 cm with uniform speed completing the circle in 4s.
View SolutionFind the magnitude of the linear acceleration of a particle moving in a circle of radius 10 cm with uniform speed completing the circle in 4s.
View SolutionThe wheel of a car is rotating at the rate of 1200 revolutions per minute. On pressing the accelerator for 10 seconds, it starts rotating at 4500 revolutions per minute. The angular acceleration of the wheel is
View SolutionA particle is moving with speed v in a circle of radius R. Find the magnitude for average velocity of point
for the half revolution
View SolutionA mass of 5kg is moving along a circular path or radius 1m. If the mass moves with 300 revolutions per minute, its kinetic energy would be
View SolutionA mass of 5kg is moving along a circular path or radius 1m. If the mass moves with 300 revolutions per minute, its kinetic energy would be
View Solution

