A machinist starts with three identical square plates but cuts one corner from one of them, two corners from the second and three corners from the third. Rank the three according to the x-coordinate of their centre of mass, from smallest to largest.

3,1,2
1,3,2
3,2,1
1 and 3tie, then 2
The correct Answer is:B
Ans. (2)
Let mass of full plate be M and cutted square plate be 'm', Xcm of cutted piece either is πt(−a) ot (+a)
(i) Xcm=M(0)−m(−a)M−m=maM−m
(ii) Xcm=M(0)−m(−a)−m(−a)M−2m=2maM−2m
(iii) Xcm=M(0)−m(−a)−m(−a)−m(−a)M−3m=maM−3m
Xcm is least for (i) and Xcm for (ii) & (iii) will be higher
Ans either 1,3,2 or 1,2,3
Also M>4m
so 1,3,2
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
Knowledge Check
In question number 45, what will be the electric field at centre O, if the charge from one of the corners (say A) is removed?
Aq4πε0r2 along OAB2q4πε0r2 along OBCq24πε0r2 along OCD2q4πε0r2 along OA
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
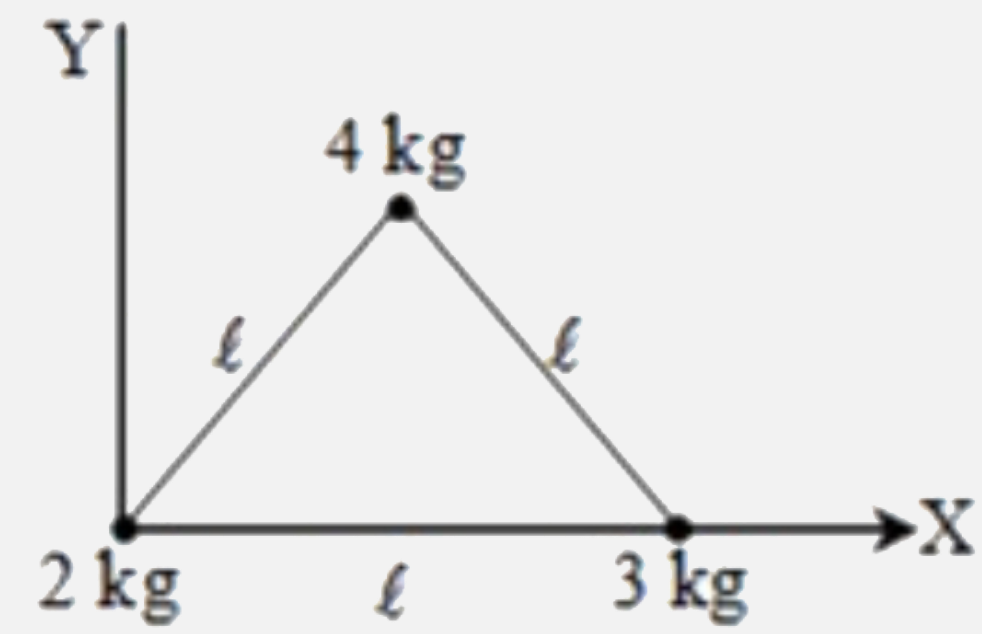
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionFour identical spheres each of radius 10 cm and mass 1 kg are placed on a horizontal surface touching one another so that their centres are located at the corners of square of side 20 cm. What is the distance of their centre of mass from centre of either sphere ?
View SolutionIf the sum of the squares of the distance of a point from the three coordinate axes is 36, then find its distance from the origin.
View SolutionIf the sum of the squares of the distance of a point from the three coordinate axes is 36, then find its distance from the origin.
View SolutionEvolution of heart from one to two, three and four chambered proves
View SolutionFour particles of masses 2,2,4,4 kg are arranged at the corners A,B,C,D of a square ABCD of side 2m as shown in the figure. The perpendicular distance of their centre of mass from the side AB is

View Solution