An airplane takes off at an angle 30∘ with the horizontal ground treveling at the speed of 180km/h. If it continuous to fly with the same velocity in the same direction, how long will it take to reach an altitude of 9km above the ground?
5 minutes
6 minutes
8 minutes
9 minutes
The correct Answer is:B
Vertical component of velocity is 180×sin30∘=90∘
time=990=110hr=6 minute
Related Playlists
Similar Questions
An elevator descends into a mine shaft at the rate of 6 m/min. If the descent starts from 10 m above the ground level, how long will it take to reach – 350 m.
View SolutionA ball is dropped from a balloon going up at a speed of 7 m/s. If the balloon was at a height 60 m at the time of dropping the ball, how long will the ball take in reaching the ground?
View SolutionA cyclist is moving with a speed of 20kmh−1 . How long will he take to travel a distance of 1.5 km ?
View SolutionAn aircraft travelling at 600km/h accelerates steady at 10 km/h per second. Taking the speed of sound as 1100 km/h at the aircraft's altitude, how long will it take to reach the sound barrier?
View SolutionAn aircraft travelling at 600km/h accelerates steady at 10 km/h per second. Taking the speed of sound as 1100 km/h at the aircraft's altitude, how long will it take to reach the sound barrier?
View SolutionA car takes 2 hours to reach a destination by travelling at the speed of 60 km/h. How long will it take when the car travels at the speed of 80 km/h?
View SolutionA ball is projected horizontally with a velocity of 5ms−1 from the top of a building 19.6m high. How long will the ball take to hit the ground ?
View SolutionA car take 6 hours to reach a distination by travelling at the speed of 50 km per hour. How long will it take when the car travels at the speed of 75 km per hour ?
View SolutionA child in danger of drowning in a river is being carried downstream by a current that flows uniformly at a speed of 2.5km/h. The child is 0.6 km from shore and 0.8 km upstream of a boat landing when a rescue boat sets out. If the boat proceeds at its maximum speed of 20km/h with respect to the water, what angle does the boat velocity v make with the shore? How long will it take boat to reach the child?
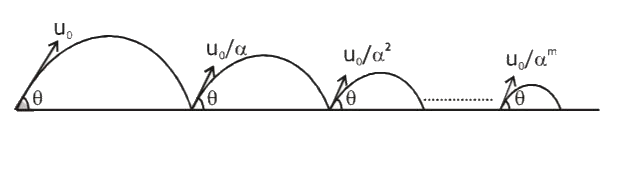
View SolutionA ball is thrown from ground at an angle θ with horizontal and with an initial speed u0 . For the resulting projectile motion, the magnitude of average velocity of the ball up to the point when it hits the ground for the first time is V1 . After hitting the ground, the ball rebounds at the same angle θ but with a reduced speed of u0 / α . Its motion continues for a long time as shown in figure. If the magnitude of average velocity of the ball for entire duration of motion is 0.8 V1 ,. the value of α is ________.
 View Solution
View Solution


