Consider the equation ddt(∫→F.d→S)=A(→F.→p) where →F≡ force, →s≡ displacement, t ≡ time and →p= momentum. The dimensional formula of A will be
M0L0T0
ML0T0
M−1L0T0
M0L0T−1
The correct Answer is:C
To find the dimensional formula of A in the equation
ddt(∫→F⋅d→S)=A(→F⋅→p),
we will analyze both sides of the equation step by step.
Step 1: Analyze the left side of the equation
The left side of the equation is
ddt(∫→F⋅d→S).
1. Understanding →F⋅d→S:
- The force →F has the unit of Newton (N), which can be expressed dimensionally as MLT−2.
- The displacement d→S has the unit of meters (m), which can be expressed dimensionally as L.
- Therefore, →F⋅d→S has the unit of N⋅m=J (Joules), which can be expressed dimensionally as ML2T−2.
2. Integrating over displacement:
- The integral ∫→F⋅d→S will also have the same units as →F⋅d→S, which is ML2T−2.
3. Differentiating with respect to time:
- When we differentiate with respect to time t, we divide by time (s), so we get:
ddt(∫→F⋅d→S) has the unit ML2T−2T=ML2T−3.
Step 2: Analyze the right side of the equation
The right side of the equation is
A(→F⋅→p).
1. Understanding →F⋅→p:
- The force →F has the unit of Newton (N), which is MLT−2.
- The momentum →p has the unit of kg⋅m/s or MLT−1.
- Therefore, →F⋅→p has the unit of:
N⋅kg⋅m/s=MLT−2⋅MLT−1=M2L2T−3.
Step 3: Equate both sides
Now we can equate the units from both sides of the equation:
ML2T−3=A⋅M2L2T−3.
Step 4: Solve for A
To isolate A, we can rearrange the equation:
A=ML2T−3M2L2T−3=1ML.
Step 5: Write the dimensional formula for A
Thus, the dimensional formula for A is:
A=M−1L−1T0.
Final Answer
The dimensional formula of A is:
M−1L−1T0.
- The force →F has the unit of Newton (N), which can be expressed dimensionally as MLT−2.
- The displacement d→S has the unit of meters (m), which can be expressed dimensionally as L.
- Therefore, →F⋅d→S has the unit of N⋅m=J (Joules), which can be expressed dimensionally as ML2T−2.
- The integral ∫→F⋅d→S will also have the same units as →F⋅d→S, which is ML2T−2.
- When we differentiate with respect to time t, we divide by time (s), so we get:
ddt(∫→F⋅d→S) has the unit ML2T−2T=ML2T−3.
- The force →F has the unit of Newton (N), which is MLT−2.
- The momentum →p has the unit of kg⋅m/s or MLT−1.
- Therefore, →F⋅→p has the unit of:
N⋅kg⋅m/s=MLT−2⋅MLT−1=M2L2T−3.
Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
If →P×→Q=→R, then which of the following statements is not true?
View SolutionThe position vector of a particle of mass m= 6kg is given as →r=[(3t2−6t)ˆi+(−4t3)ˆj]m. Find:
(i) The force (→F=m→a) acting on the particle.
(ii) The torque (→τ=→r×→F) with respect to the origin, acting on the particle.
(iii) The momentum (→p=m→v) of the particle.
(iv) The angular momentum (→L=→r×→p) of the particle with respect to the origin.
View Solution
Knowledge Check
Poynting vectors →S is defined as →S=1μ0→E×→B. The average value of '→S' over a single period 'T' is given by
AE20/2cμ0BE20/cμ0C2E022/cμ0DE20/cμ20
A smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
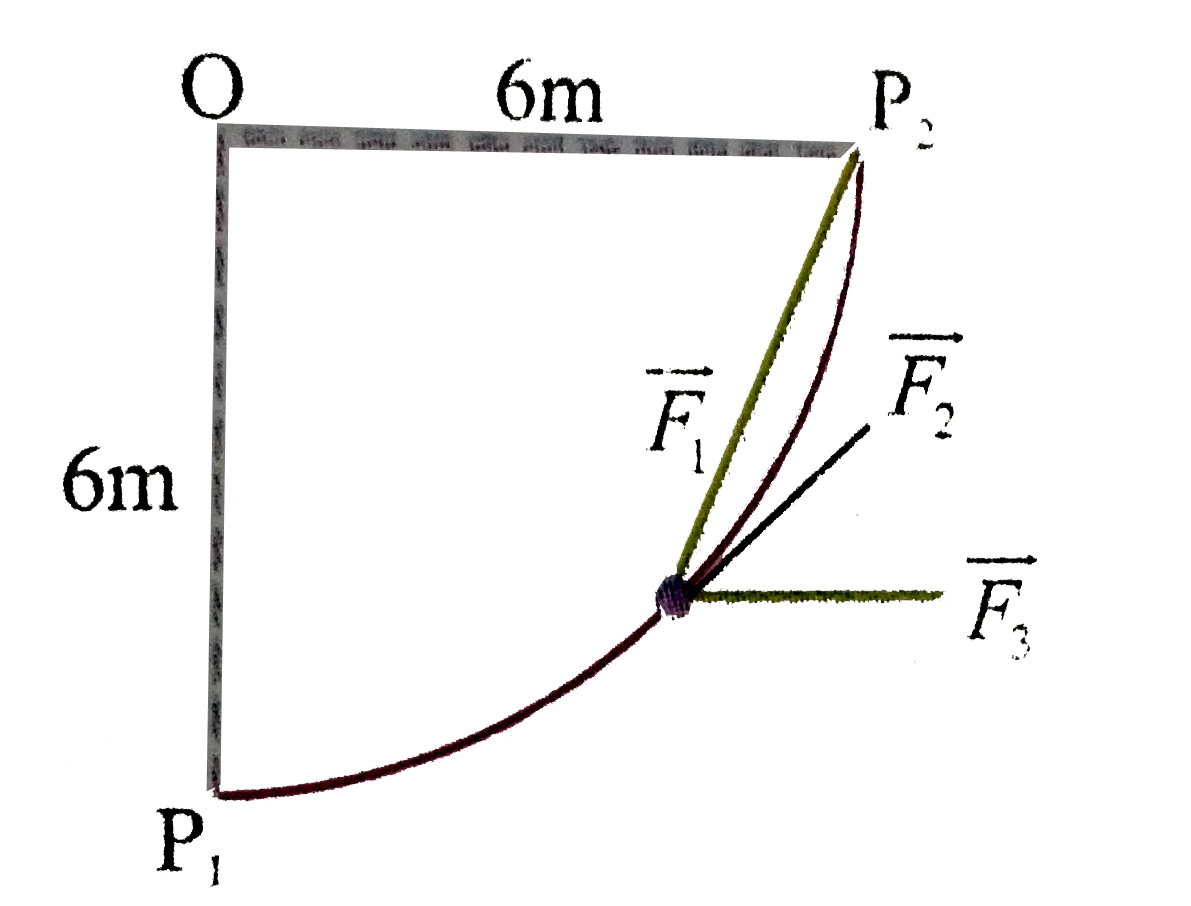 .
.
View SolutionA particle which is experiencing a force, given by →F=3→i−12→j, undergoes a displacement of →d=4→i. If the particle had a kinetic energy of 3 J at the beginning of the displacement
View SolutionA particle performs SHM along a straight line and its position is →R, acceleration is →a, velocity is →v is and force on particle is →f. Then which of the following statement are true?
(i) →v.→a is always + ve
(ii) →v.→R may be -ve
(iii) →f.→R is always -ve
(iv) →v is parallel to →f sometimes
View SolutionABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is

View SolutionA body is acted upon by a force →F, given by
→F=−k[(cosωt)ˆi+(sinωt)ˆi] undergoes displacement, where the position vector
→r of the body is given by →r=a[cos(ωt+α)ˆi+sin(ωt+α)ˆj]. Find the work done by the force from time t=0 to time t=2π/ω.
View SolutionThe resultant vector of →P and →Q is →R. On reversing the direction of →Q the resultant vector becomes →S. Show that R2+S2=2(P2+Q2)
View SolutionA particle of m=5kg is momentarily at rest at x=att=. It is acted upon by two forces →F1 and →F2. Vec(F)1=70ˆj N. The direction and manitude of →F2 are unknown. The particle experiences a constant acceleration, →a,in the direction as shown in (figure) Neglect gravity.
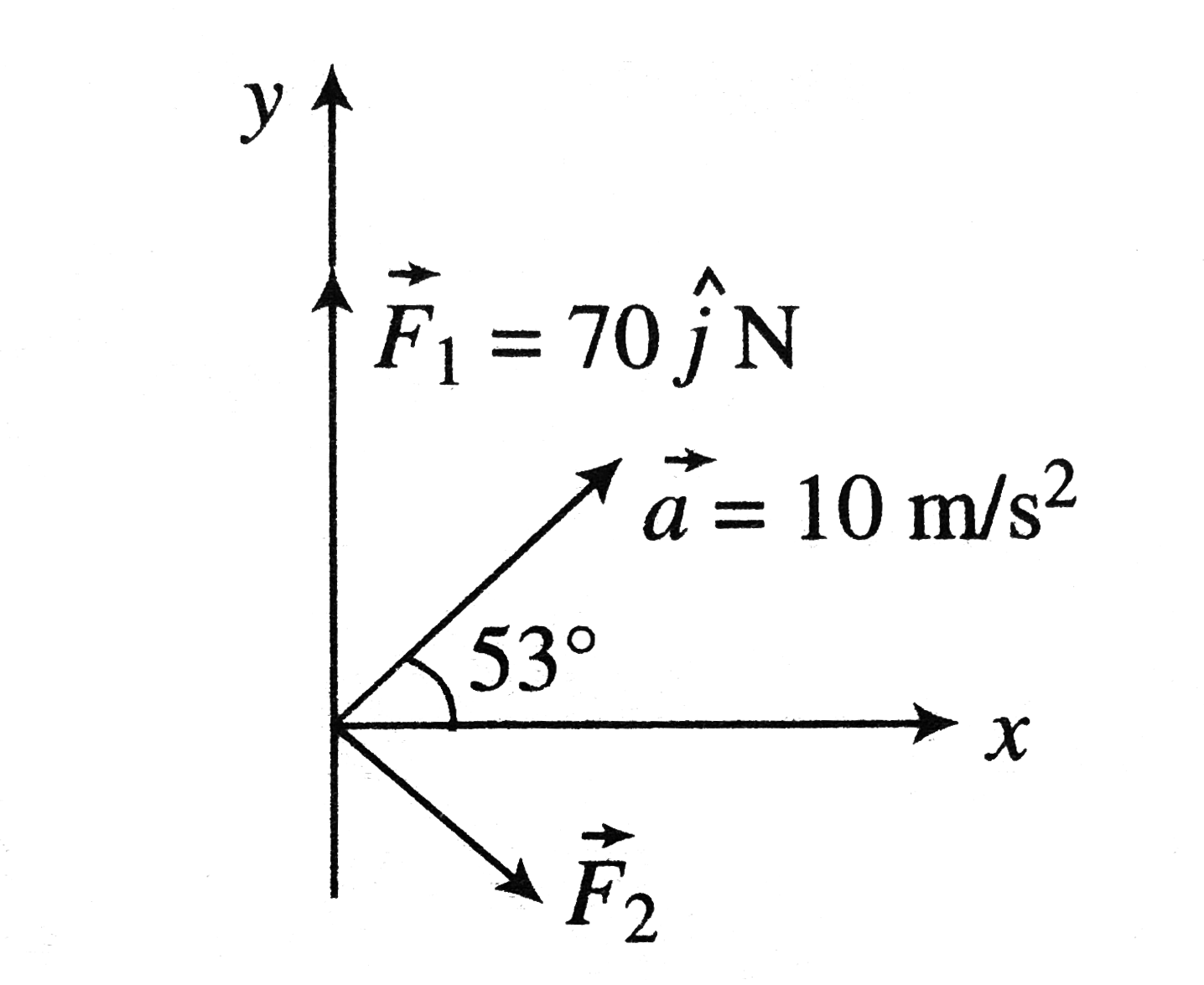
a.Find the missing force →F2.
b. What is the velocity vector of the particle at t=10s?
c. What third force, →F3 is required to make the acceleration of the particle zero? Either give magnitude and direction of →F3 or its components.
View Solution