A particle of mass m is moving with constant speed in a vertical circle in X−Z plane. There is a small both at some distance on Z−axis. The maximum distance of the shadow of the particle on X−axis from origin equal to :−
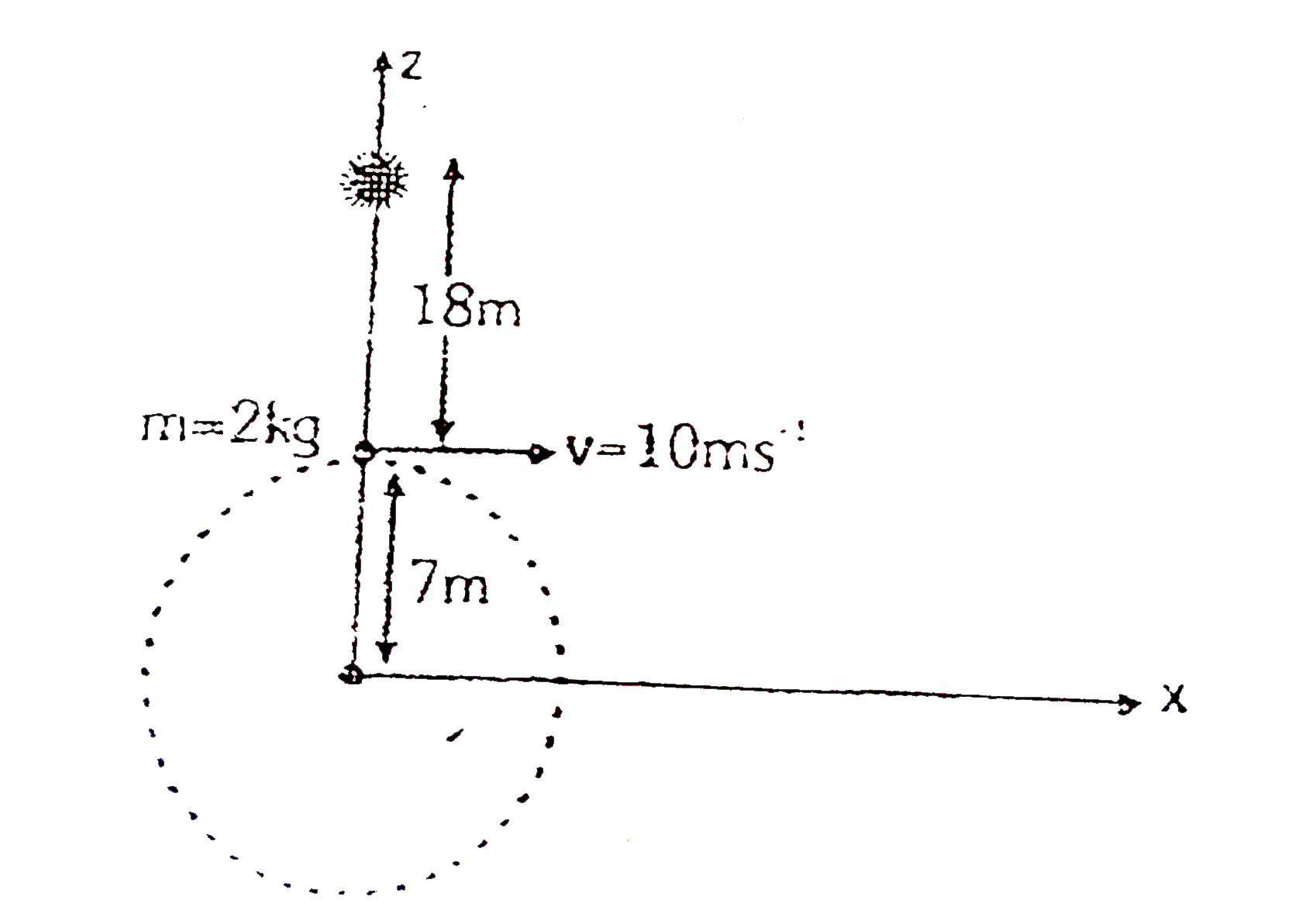
17524m
12524m
25m
24m
The correct Answer is:A
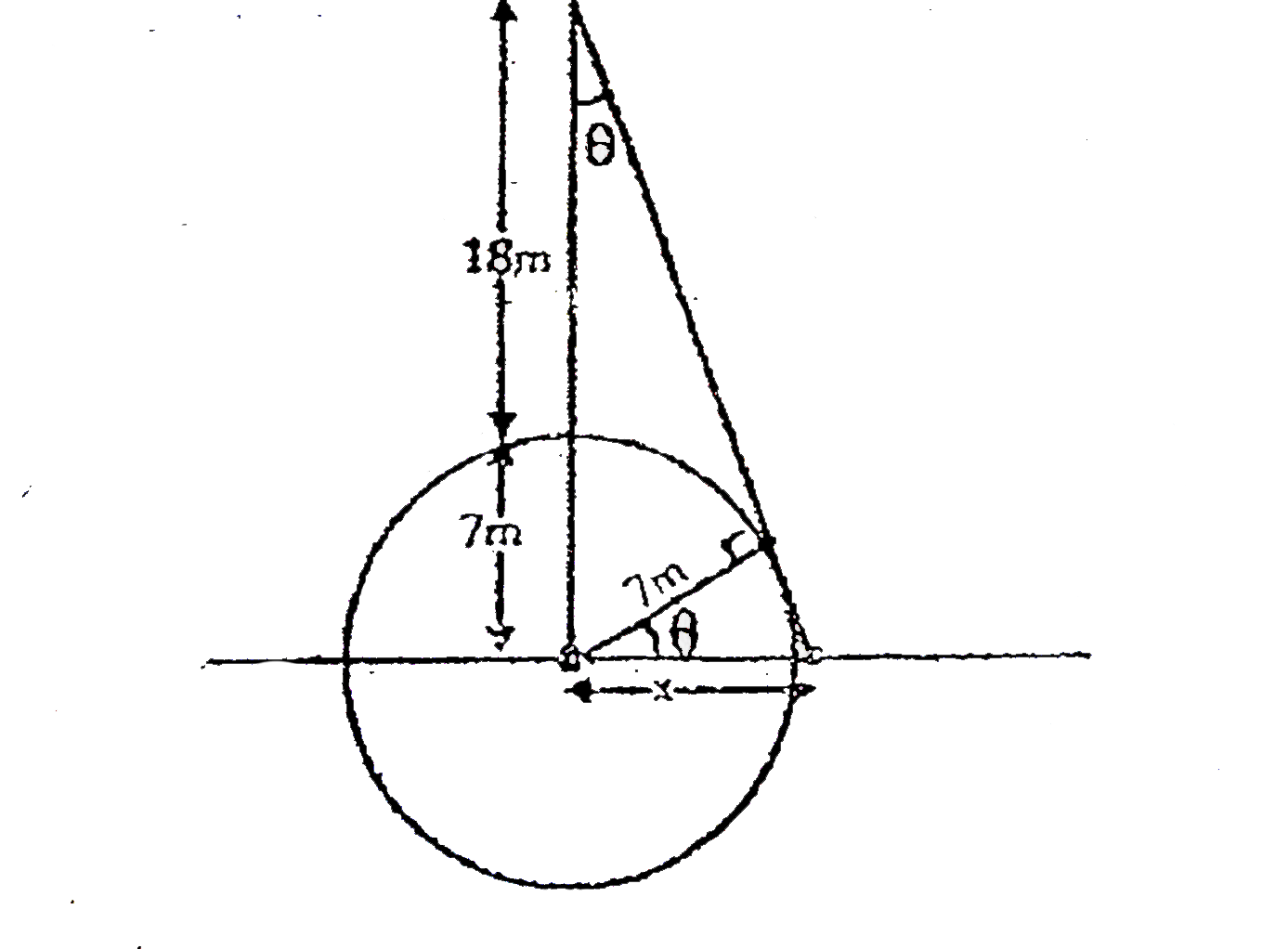
sinθ=725,cosθ=2425
xcosθ=7⇒x=7cosθ=7×2524=17524m
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
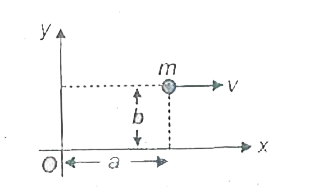
A particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
View SolutionA particle of mass m is moving with speed u. It is stopped by a force F in distance x if the stopping force is 4 F then
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionIn the previous question, if the pitch of the helical path is equal to the maximum distance of the particle from the x-axis
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on horizontal plane move in a simple harmonic motion?
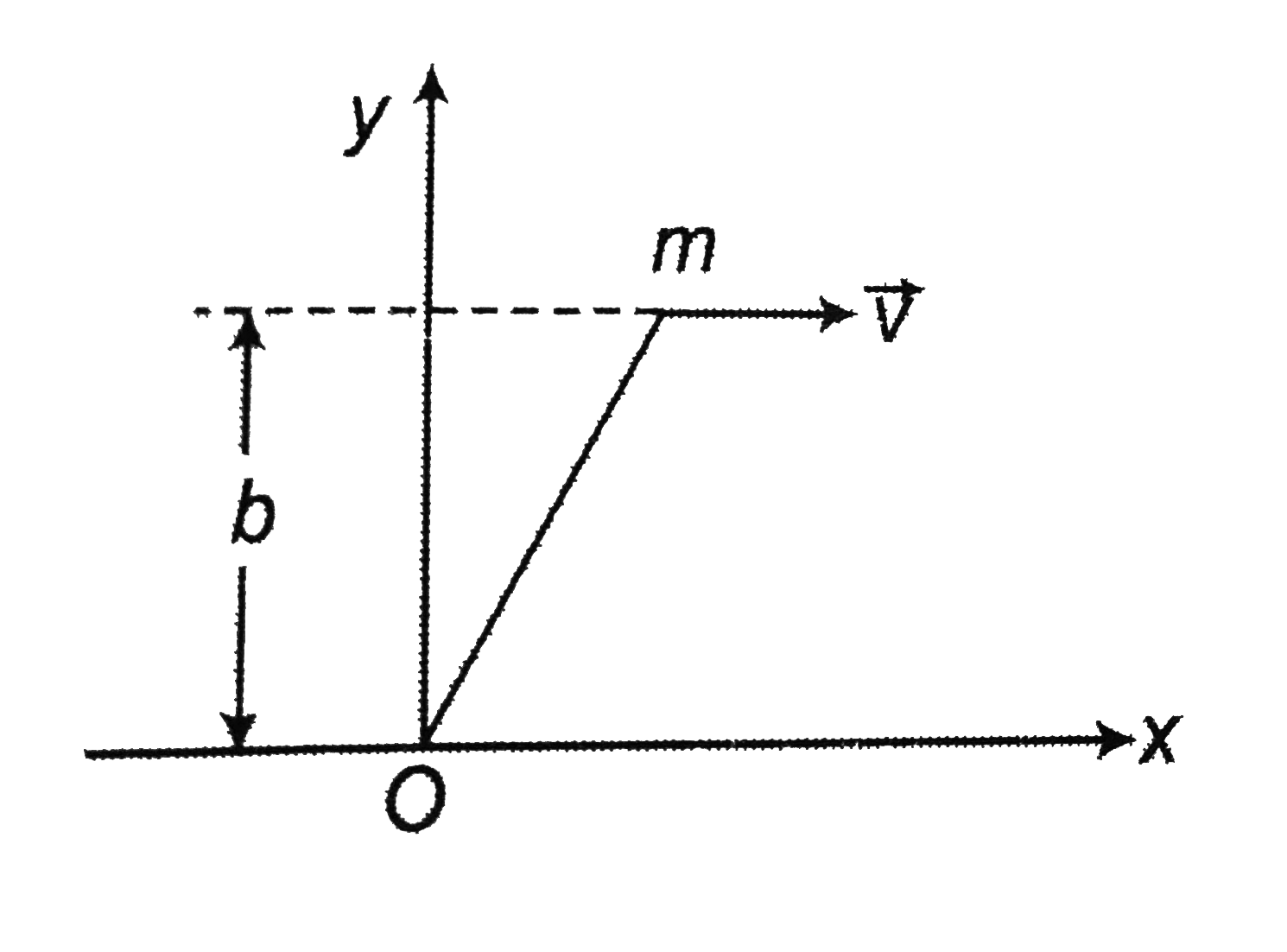
View SolutionIf the particle of mass m is moving with constant velocity v parallel to x-axis in x-y plane as shown in (figure), Find its angular momentum with respect of origin at any time t.
View SolutionA particle of mass m is released in vertical plane from a point P at x=x0 on the x-axis. It falls vertically parallel to the y-axis. Find the torque τ acting on the particle at a time about origin.

View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionA particle of mass m is moving along the line y=b,z=0 with constant speed v. State whether the angular momentum of particle about origin is increasing, decreasing or constant.
View Solution
