A plane body has perpendicular axes OX and OY marked on it and is acted on by following forces 5P in the direction OY, 4P in the direction OX, 10P in the direction OA where A is the point (3a,4a) 15 P in the direction AB where B is the point (−a,a).
Express each force in the vector form & calculate the magnitude & direction of the vector sum of these forces.
The correct Answer is:5Pˆj,4Pˆi,6Pˆi+8Pˆj,−12Pˆi−9Pˆj,√20P,tan−1[−2] with +ve x-axis
To solve the problem step by step, we will express each force in vector form and then calculate the vector sum of these forces. Finally, we will determine the magnitude and direction of the resultant vector.
Step 1: Express each force in vector form
1. Force F1 (5P in the direction OY):
- This force acts along the Y-axis.
- Vector form: →F1=5P^j
2. Force F2 (4P in the direction OX):
- This force acts along the X-axis.
- Vector form: →F2=4P^i
3. Force F3 (10P in the direction OA):
- Point A is given as (3a, 4a). The direction vector OA can be expressed as →OA=3^i+4^j.
- The magnitude of OA is √(32+42)=5.
- Therefore, the unit vector in the direction of OA is 3^i+4^j5.
- Thus, the vector form of F3 is:
→F3=10P⋅3^i+4^j5=6P^i+8P^j
4. Force F4 (15P in the direction AB):
- Point B is given as (-a, a). The direction vector AB can be expressed as →AB=(−a−3a)^i+(a−4a)^j=−4a^i−3a^j.
- The magnitude of AB is √(−4a)2+(−3a)2=5a.
- Therefore, the unit vector in the direction of AB is −4^i−3^j5.
- Thus, the vector form of F4 is:
→F4=15P⋅−4^i−3^j5=−12P^i−9P^j
Step 2: Calculate the vector sum of the forces
Now, we sum all the force vectors:
→F=→F1+→F2+→F3+→F4
Substituting the values:
→F=(5P^j)+(4P^i)+(6P^i+8P^j)+(−12P^i−9P^j)
Combining like terms:
→F=(4P+6P−12P)^i+(5P+8P−9P)^j
→F=(−2P)^i+(4P)^j
Step 3: Calculate the magnitude of the resultant vector
The magnitude of the vector →F is given by:
|→F|=√(−2P)2+(4P)2=√4P2+16P2=√20P2=√20P=2√5P
Step 4: Calculate the direction of the resultant vector
The direction (angle α) can be found using the tangent function:
tanα=FyFx=4P−2P=−2
Thus,
α=tan−1(−2)
Final Answer
The vector sum of the forces is:
→F=−2P^i+4P^j
The magnitude of the resultant vector is:
|→F|=2√5P
The direction of the resultant vector is:
α=tan−1(−2)
- This force acts along the Y-axis.
- Vector form: →F1=5P^j
- This force acts along the X-axis.
- Vector form: →F2=4P^i
- Point A is given as (3a, 4a). The direction vector OA can be expressed as →OA=3^i+4^j.
- The magnitude of OA is √(32+42)=5.
- Therefore, the unit vector in the direction of OA is 3^i+4^j5.
- Thus, the vector form of F3 is:
→F3=10P⋅3^i+4^j5=6P^i+8P^j
- Point B is given as (-a, a). The direction vector AB can be expressed as →AB=(−a−3a)^i+(a−4a)^j=−4a^i−3a^j.
- The magnitude of AB is √(−4a)2+(−3a)2=5a.
- Therefore, the unit vector in the direction of AB is −4^i−3^j5.
- Thus, the vector form of F4 is:
→F4=15P⋅−4^i−3^j5=−12P^i−9P^j
→F=→F1+→F2+→F3+→F4
Substituting the values:
→F=(5P^j)+(4P^i)+(6P^i+8P^j)+(−12P^i−9P^j)
Combining like terms:
→F=(4P+6P−12P)^i+(5P+8P−9P)^j
→F=(−2P)^i+(4P)^j
|→F|=√(−2P)2+(4P)2=√4P2+16P2=√20P2=√20P=2√5P
tanα=FyFx=4P−2P=−2
Thus,
α=tan−1(−2)
→F=−2P^i+4P^j
The magnitude of the resultant vector is:
|→F|=2√5P
The direction of the resultant vector is:
α=tan−1(−2)
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-4[B]
14 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-5(A)
15 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - DATA SUFFICIENCY QUESTIONS
3 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
The direction of the field B at P is

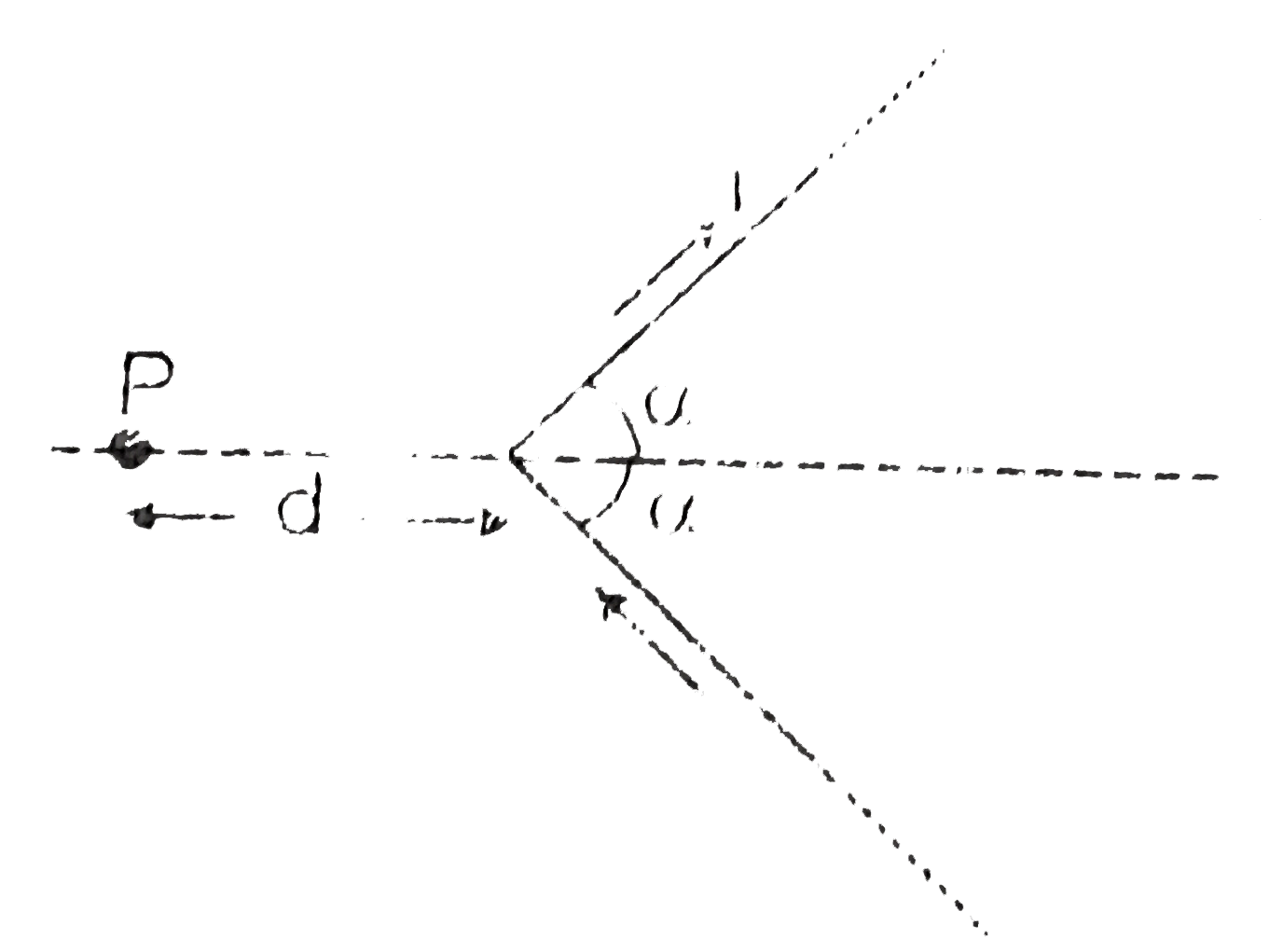
View SolutionFind the direction cosines of the vector joining the points A(1,2,3)andB(1,2,1), directed from A to B.
View SolutionEvaluate magnitude and direction of magnetic field at a point P in the following cases
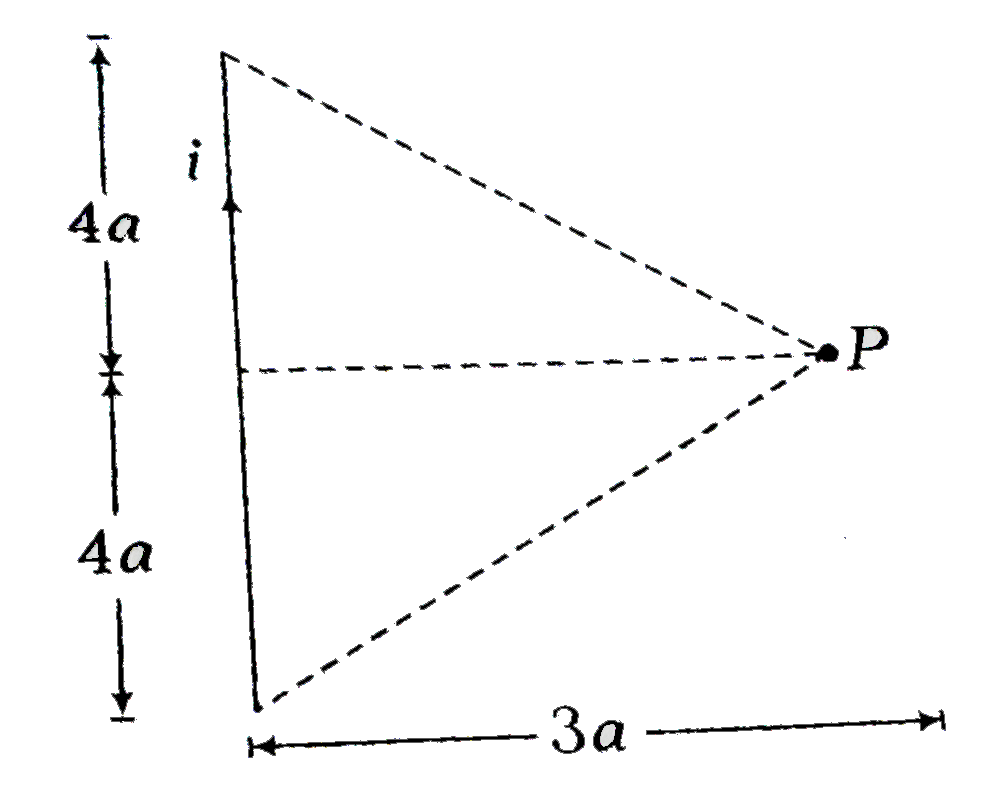

View SolutionFind the direction COSINES of the line joining the points P(4,3,−5)andQ(−2,1,−8)
View SolutionFind the direction ratios and direction cosines of a line joining the points (3,−4,6) and (5,2,5).
View SolutionFind the direction cosines of the vector joining the points A(1,2,−3)andB(−1,−2,1) directed from A to B.
View SolutionA body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N Give the magnitude and direction of the acceleration of the body.
View SolutionAn object moves from position (3,4) to (6,5) in the xy-plane. Find the magnitude and direction of displacement vector of the particle.
View SolutionFind the unit vector in the direction of vector →PQ , where P and Q are the points (1,2,3) and (4,5,6), respectively.
View SolutionFind the unit vector in the direction of vector →PQ , where P and Q are the points (1,2,3) and (4,5,6), respectively.
View Solution
