Vector →a has components ax=3,ay=4. The components of a vector →c which is perpendicular to →a and has magnitude of 5 unit will be :
The correct Answer is:cx=±4,cy=±3
Let →c is =cxˆi+cyˆj
then according to question =√c2x+c2y=5
⇒c2x+c2y=25 …(i)
and →a,→c=0⇒3cx+4cy=0− …(ii)
from equation (i) and (ii) cx=±4,cy=±3
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-4[B]
14 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-5(A)
15 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - DATA SUFFICIENCY QUESTIONS
3 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
Vector →a has components ax=3,ay=4. Find the components of a vector →c which is perpendicular to →a and has a magnitude of 5 units.
View SolutionThe component of →A=ˆi+ˆj+5ˆk perpendicular to →B=3ˆi+4ˆj is
View SolutionWhich of the following is the unit vector perpendicular to →A and →B?
View SolutionThe resultant of two vectors →P and →Q is →R. If →Q is doubled then the new resultant vector is perpendicular to →P. Then magnitude of →R is :-
View SolutionTwo vectors →P and →Q are added, the magnitude of resultant is 15 units. If →Q is reversed and added to →P resultant has a magnitude √113 units. The resultant of →P and a vector perpendicular →P and equal in magnitude to→Q has a magnitude
View SolutionWhat is the component of the vector →a along the x-axis in the situation shown in figure ? |→a|=5 units.
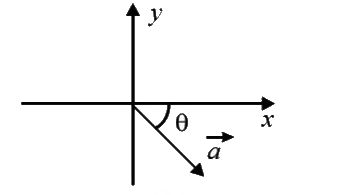
View SolutionA vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
View SolutionIf →aand→b are two vector such that ∣∣→a+→b∣∣=|→a|, then show that vector |2a+b| is perpendicular to →b.
View SolutionIf a vector →a is perpendicular to two non-collinear vector →b and →c , then →a is perpendicular to every vector in the plane of →b and →c .
View SolutionThere are two vector →A=3ˆi+ˆj and →B=ˆj+2ˆk. For these two vectors-
(i) Find the component of →A along →B and perpendicular to →B in vector form.
(ii) If →A & →B are the adjacent sides of parallelogram then find the magnitude of its area.
(iii) Find a unit vector which is perpendicular to both →A & →B.
View Solution
