The resultant of two vectors →P and →Q is →R. If →Q is doubled then the new resultant vector is perpendicular to →P. Then magnitude of →R is :-
P2−Q22PQ
Q
PQ
P+QP−Q
The correct Answer is:B
→R=→P+→Q,→R'=→P+2→Q
∵→R'.→P=0∴(→P+2→Q).→P=0⇒P2+2→Q.→P=0
R2=P2+Q2+2→P.→Q=P2+Q2−P2=Q2⇒R=Q
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-037videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - ASSERTION-REASON18videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
The resultant of vectors −−→OAand−−→OB is perpendicular to −−→OA. Find the angle AOB.
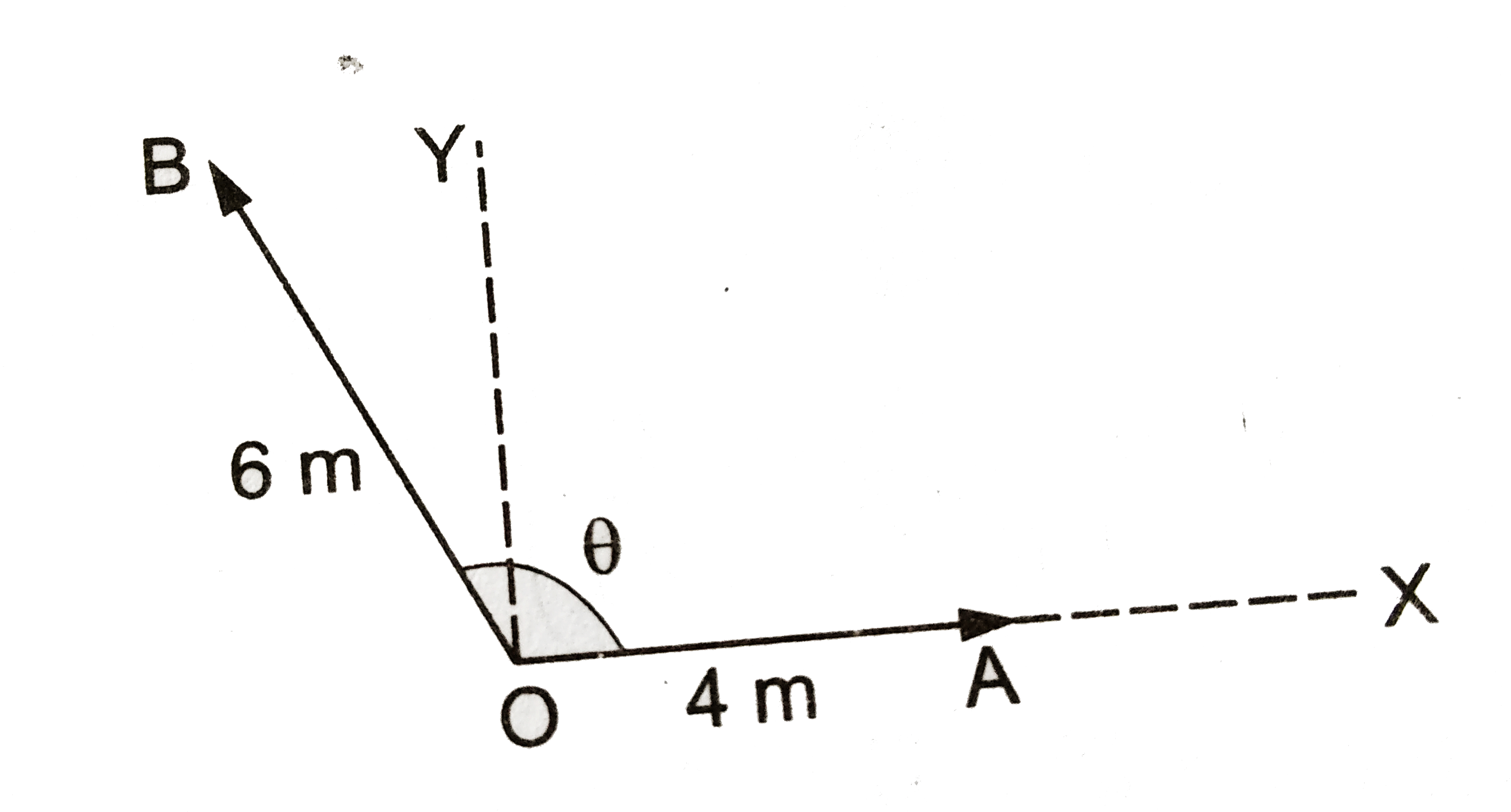 View Solution
View SolutionThe resultant of →P and →Q is →R. If →Q is doubled, →R is doubled, when →Q is reversed, →R is again doubled. Find P:Q:R.
View SolutionThe resultant and dot product of two vectors →aand→b is equal to the magnitude of →a. Show that when the vector →a is doubled , the new resultant is perpendicular to →b .
View SolutionIf →aand→b are two vector such that ∣∣→a+→b∣∣=|→a|, then show that vector |2a+b| is perpendicular to →b.
View SolutionThe resultant vector of →P and →Q is →R. On reversing the direction of →Q the resultant vector becomes →S. Show that R2+S2=2(P2+Q2)
View SolutionThe resultant →Pand→Q is perpendicular to →P. What is the angle between →Pand→Q?
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
 View Solution
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ , find the angle between →P and →Q.
View SolutionIf →a,→b are two vectors such that ∣∣→a+→b∣∣=∣∣→b∣∣, then prove that →a+2→b is perpendicular to →a .
View SolutionIf two vectors →aand→b are such that ∣∣→a.→b∣∣=∣∣→a×→b∣∣, then find the angle the vectors →aand→b
View Solution
