A bird moves from point (1m,−2m,3m) to (4m,2m,3m). If the speed of the bird is 10m/s, then the velocity vector of the bird in m/s is:
5(ˆi−2ˆj+3ˆk)
5(4ˆi+2ˆj+3ˆk)
0.6ˆi+0.8ˆj
6ˆi+8ˆj
The correct Answer is:D
To find the velocity vector of the bird moving from point A(1,−2,3) to point B(4,2,3) with a speed of 10m/s, we can follow these steps:
Step 1: Determine the displacement vector
The displacement vector →AB from point A to point B can be calculated using the formula:
→AB=→B−→A
Where:
- →A=(1,−2,3)
- →B=(4,2,3)
Calculating the components:
→AB=(4−1,2−(−2),3−3)=(3,4,0)
Step 2: Write the displacement vector in unit vector form
The displacement vector can be expressed as:
→AB=3^i+4^j+0^k
Step 3: Calculate the magnitude of the displacement vector
The magnitude |→AB| of the displacement vector is given by:
|→AB|=√(3)2+(4)2+(0)2=√9+16+0=√25=5
Step 4: Find the unit vector in the direction of the displacement
The unit vector ^u in the direction of →AB is calculated as:
^u=→AB|→AB|=3^i+4^j+0^k5=35^i+45^j
Step 5: Calculate the velocity vector
The velocity vector →v is given by the product of the speed and the unit vector:
→v=speed×^u=10m/s×(35^i+45^j)
Calculating this gives:
→v=10×35^i+10×45^j=6^i+8^j
Final Answer
Thus, the velocity vector of the bird is:
→v=6^i+8^jm/s
---
The displacement vector →AB from point A to point B can be calculated using the formula:
→AB=→B−→A
Where:
- →A=(1,−2,3)
- →B=(4,2,3)
→AB=(4−1,2−(−2),3−3)=(3,4,0)
The displacement vector can be expressed as:
→AB=3^i+4^j+0^k
The magnitude |→AB| of the displacement vector is given by:
|→AB|=√(3)2+(4)2+(0)2=√9+16+0=√25=5
The unit vector ^u in the direction of →AB is calculated as:
^u=→AB|→AB|=3^i+4^j+0^k5=35^i+45^j
The velocity vector →v is given by the product of the speed and the unit vector:
→v=speed×^u=10m/s×(35^i+45^j)
Calculating this gives:
→v=10×35^i+10×45^j=6^i+8^j
Thus, the velocity vector of the bird is:
→v=6^i+8^jm/s
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exersice-03
Explore 7 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:ASSERTION-REASON
Explore 18 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example Some worked out Examples
Explore 1 Video
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
Knowledge Check
A bird flies from (-3m, 4m, -3 m) to (7m, -2m, -3m) in the xyz-coordinates. The bird's displacement vector is given by
A(4ˆi+2ˆj−6ˆk)B(10ˆi−6ˆj)C(4ˆi−2ˆj)D(10ˆi+6ˆj−6ˆk)A body sends waves 100mm long through medium A and 0.25m long in medium B. If the velocity of waves in medium A is 80cms−1, calculate the velocity of waves in medium B. a) 1 m/s b) 2 m/s c) 3 m/s d) 4 m/s
A1ms−1B2ms−1C3ms−1D4ms−1A boy aims a gun at a bird from a point, at a horizontal distance of 100 m. If the gun can impart a velocity of 500 m/sec to the bullet, at what height above the bird must be aim his gun in order to hit it ?
A400 m/sB200 m/sC800 m/sD256 m/s
A particle is projected with initial velocity u=10m/s from a point ( 10m, 0m, 0m ) m along z-axis. At the same time , another particle was also projected with velocity v(ˆi−ˆj+ˆk)m/s from ( 0m, 10m, 0m). It is given that they collide at some point in the space . Then find the value of v. [→g=10m/s2(−ˆk)]
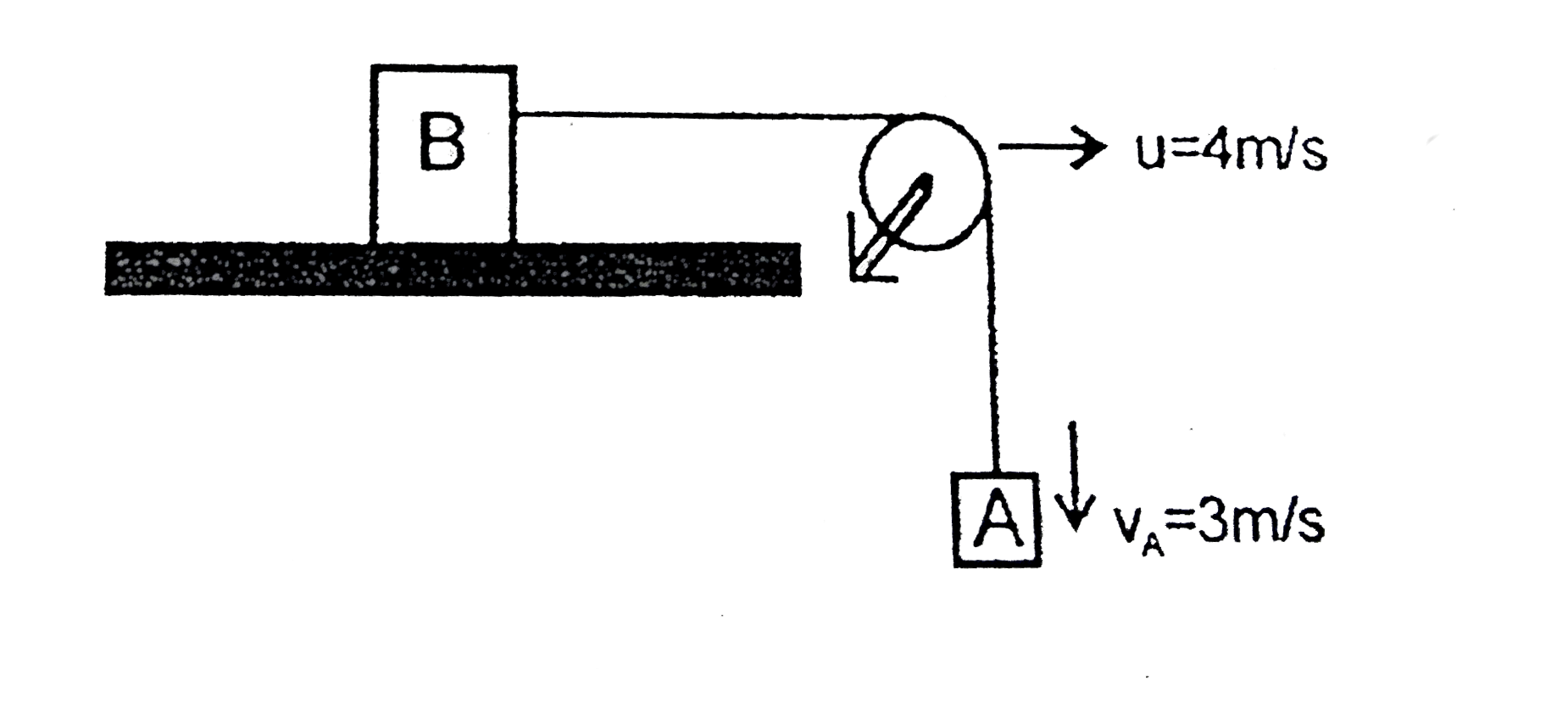
View SolutionIn the figure, the pulley P moves to the right with a constant speed of 4m/s. The downward speed of A is vA=3m/s. Then find the speed of B of the right (in m/s).
View SolutionA particle moves in xy-plane from position (2m, 4m) to (6m,8m) is 2s. Magnitude and direction of average velocity is
View SolutionA point sourcs S is moving with a speed of 10m/s in x−y plane as shown in the figure. The radius of curvature of the concave mirror is 4m. Determine the velocity vector of the image formed by paraxial rays.
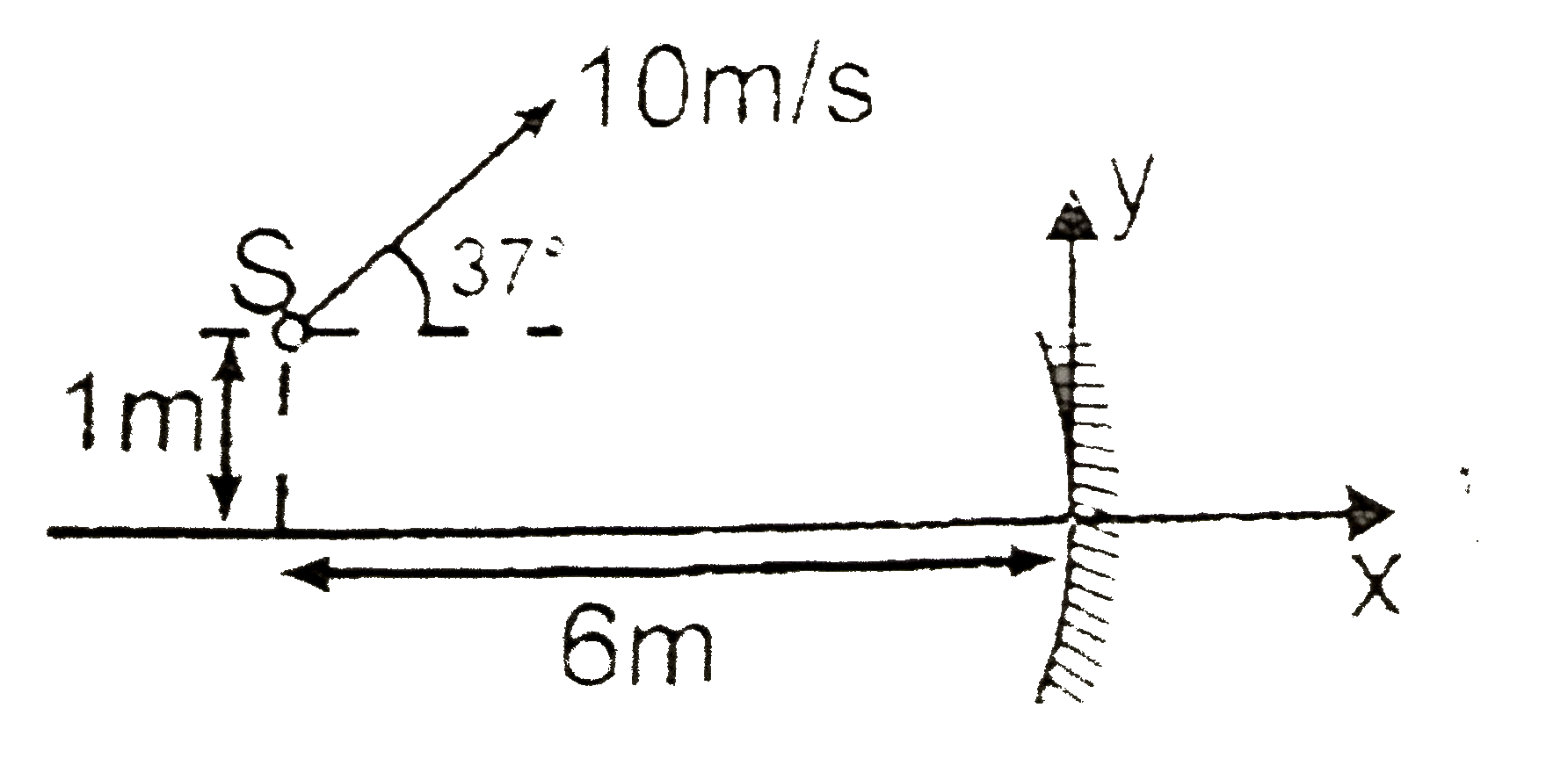
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View Solution
