An optical fiber has index of refraction n=1.40 and diameter d=100μm. It is surrounded by air. Light is sent into the fiber along the axis as shown in figure. If smallest outside radius R permitted for a bend in the fiber for no light to escape is given by 50x(inμm) fill value of x.

The correct Answer is:7
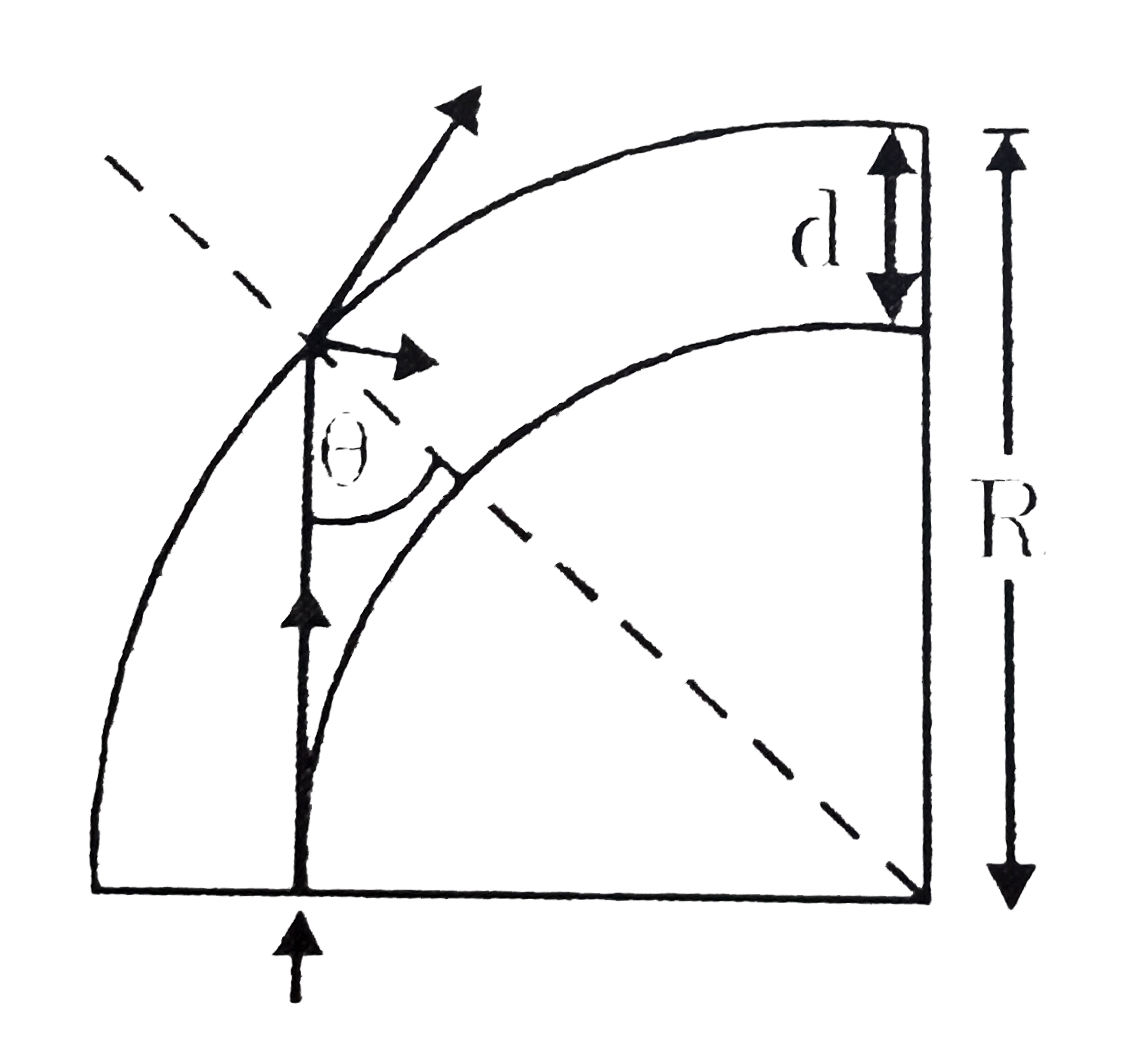
A ray along the inner edge will escape. Its angle of incidence is described by sinθ=R−dR and by n sinθ>sin90^(@)<br>Then(n(R-d))/(R ) gt 1 nR - nd gt R nR -R gt nd R gt (nd)/(n-1)<br>R_(min) =(1.40(100xx10^(-6)m))/(0.40) =350xx 10^(-6)m
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
17 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
71 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A cylinderical optical fibre (quarter circular shape) of refractive index n=2 and diameter d=4mm is surrounded by air. A light beam is sent into the fibre along its axis as shown in figure. Then the smallest outer radius R (as shown in figure) for which no light escapes after incident on curved surface of fibre is:
 .
.
View SolutionYDSE is carried out in a liquid of refractive index μ=1.3 and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. Find the positions of the fourth maxima. The wavelength of light is air is λ0=0.78μm and D/d=1000.
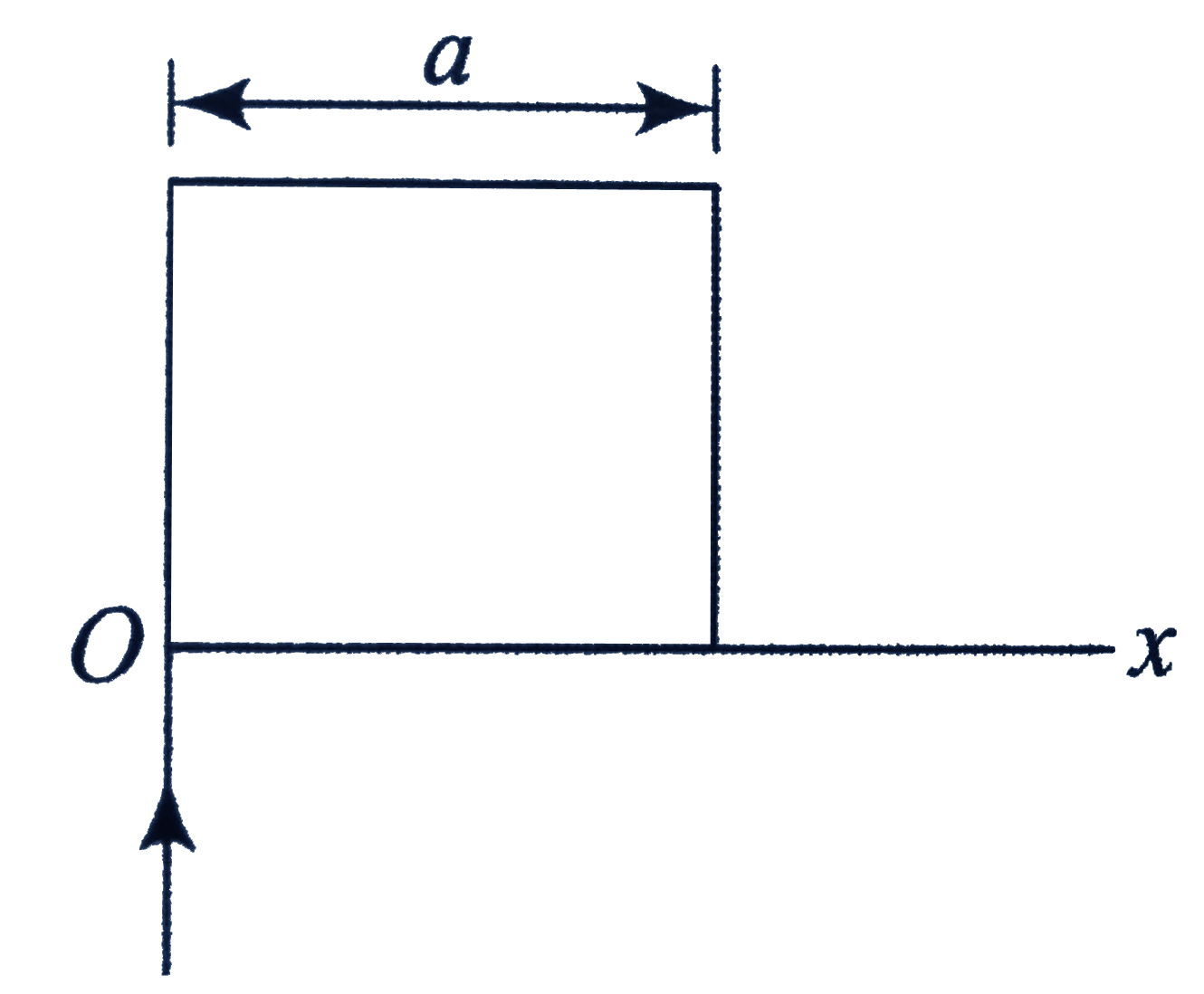
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View SolutionA satellite is launched into a circular orbit of radius R around the earth while a second satellite is launched into an orbit of radius 1.02R. The percentage difference in the time period is:
View SolutionIn a Young's double slit experiment, the light sources is at distance l1=20μm and l2=40μm form the main slit. The light of wavelength lambda = 500nm is incident on slits separated at a distance 10μm. A screen is placed at a distance D = 2 away from the slits as shown in figure. Find
(a) the values of θ relative to the central line where maxima appear on the screen?
(b) how many maxima will appear on the screen?
what should be the minimum thickness of a slab of refractive index 1.5 placed on the path of one of the ray so that minima occurs at C ?
 .
.
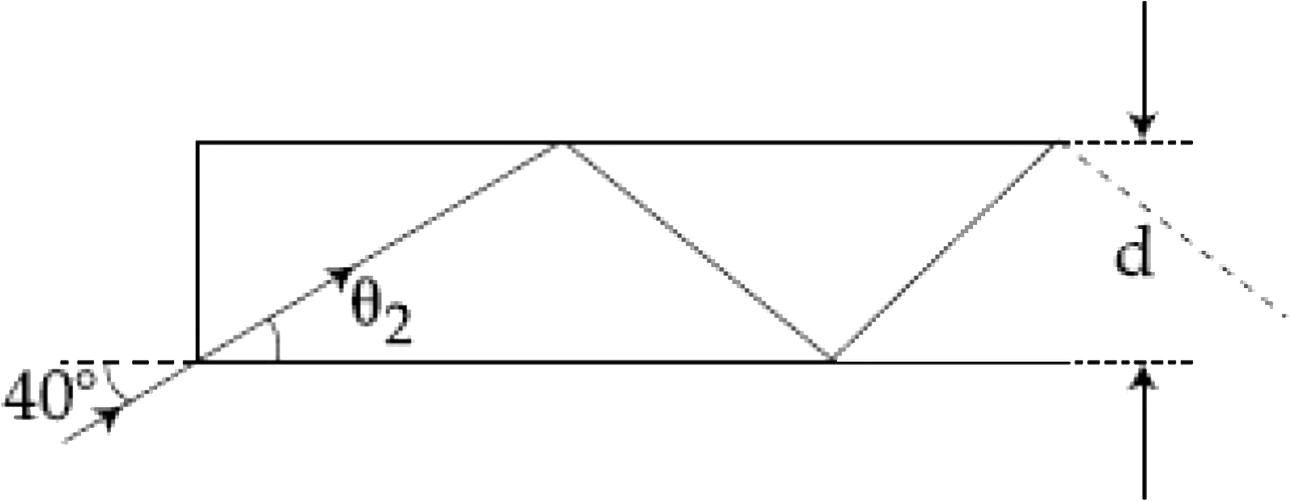
View SolutionIn figure, the optical fiber is I=2m long and has a diameter of d=20μm. If a ray of light is incidnet on one end of the fiber at angle 01=40∘C, the number of reflections if makes before emerging from the other and is close to:
(refractive index of fiber is 1.31 and sin40∘=0.64)
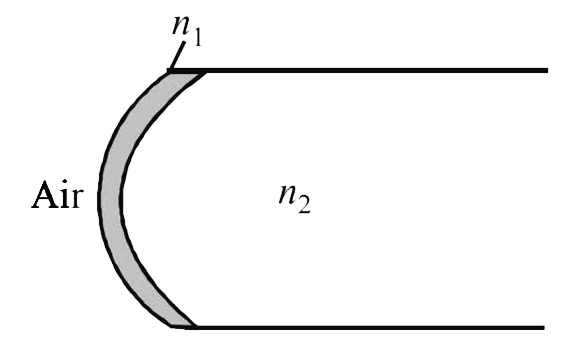
View SolutionWhat is the least radius through which an optical fiber of core diameter 0.05 mm may be bent (as shown in figure) without serious loss of light? The refractive index of the core is 1.6 and that of cladding is 1.5.
_E01_020_Q01.png)
View SolutionA light source S is placed at the centre of a glass sphere of radius R and refractive index μ. The maximum angle θ with the x-axis (as shown in the figure) an incident light ray can make without suffering total internal reflection is

View SolutionA transparent thin film of uniform thickness and refractive index n1=1.4 is coated on the convex spherical surface of radius R at one end of a long solid glass cylinder of refractive index n2=1.5, as shown in the figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance f1 from the film, while rays of light traversing from glass to air get focused at distance f2 from the film, Then
View SolutionA right angled prism of refractive index μ1 is placed in a rectangular block of refractive index μ2 , which is surrounded by a medium of refractive index μ3 ,as shown in the figure . A ray of light 'e' enters the rectangular block at normal incidence . depending upon the relationship between μ1,μ2andμ3 , it takes one of the four possible paths 'ef' , 'eg' , 'eh' or 'ef'
_E01_228_Q01.png)
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists:
{:("List" I , "List" II) , ( P. e rarr f , 1. mu_(1)gt sqrt(2mu_(2))) , ( Q. e rarr g , 2. mu_(2) gt mu_(1) "and" mu_(2) gt mu_(3)), ( R. e rarr f , 3. mu_(1) = mu_(2)), ( S. e rarr f , 4. mu_(2) lt mu_(1) lt sqrt(2mu_(2)) "and" mu_(2) gt mu_(3)):}<br>Codes:<br>{:( P , Q , R , S) , ((A) 2 , 3 , 1 , 4), ((B) 1 , 2 , 4 , 3) , ((C) 4 , 1 , 2 , 3) , ((D) 2, 3 , 4 , 1):}
View Solution
