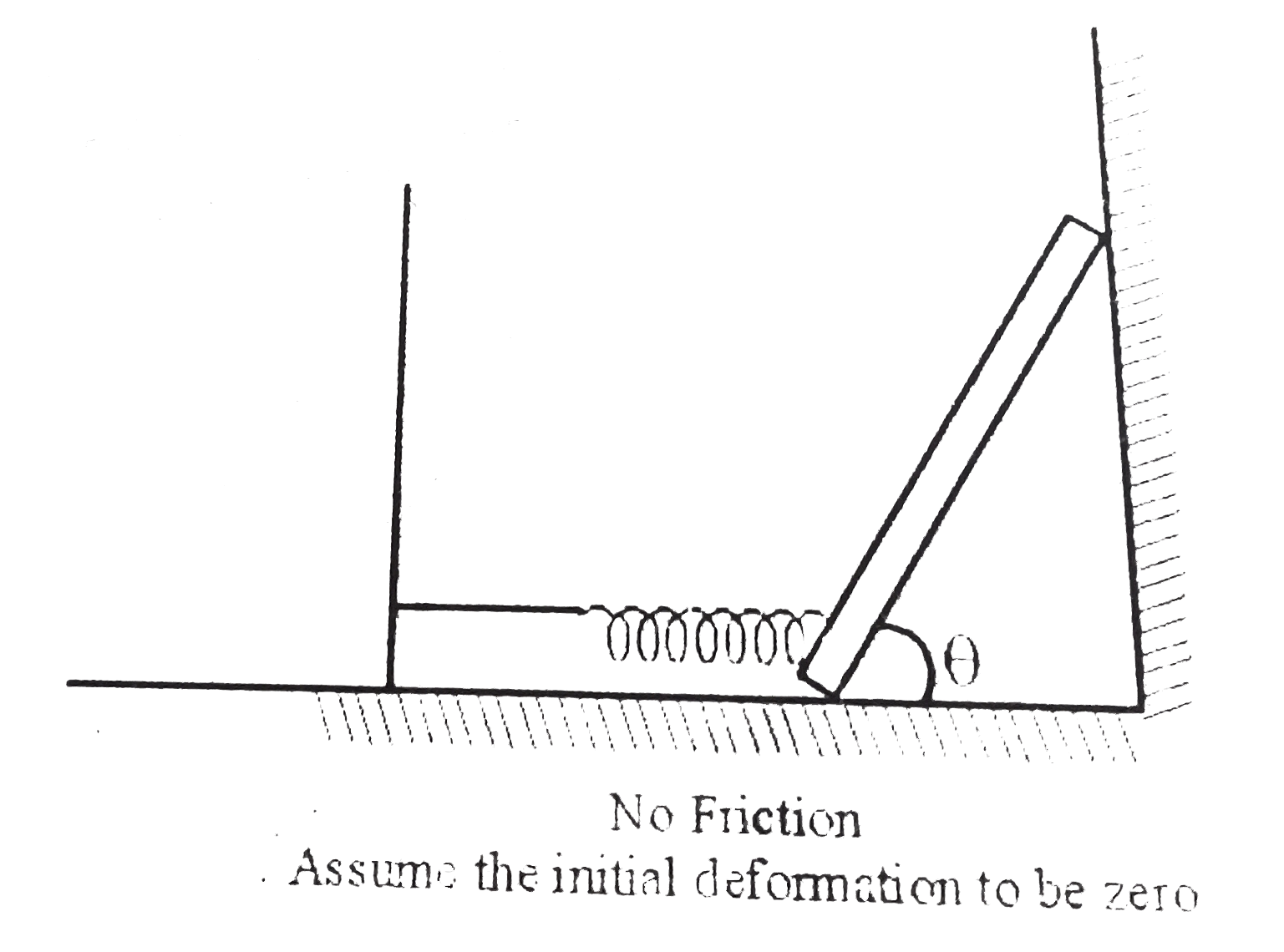
In the diagram shown below, the rod is uniform having mas M and length L. When it is making an angle =60∘ the rod is released from the state of rest (and spring in its natural lenth) The rod comes to state of rest when the angle theta reduces to 30∘. What should be the initial compression in the spring (when θ=60∘) so that the whole system can remain in the state of rest? (there is no friction between any surfaces)
(√3−1)2√3
3√3−12l
(√3−1)4√3l
2√3−1√3l
The correct Answer is:C
mg,12(sin60−sin30)=12kx2
x=lcos30−lcos60
=mg,12(√32−12)=12kl2(√32−12)2
=2mgl(√3−1)=k
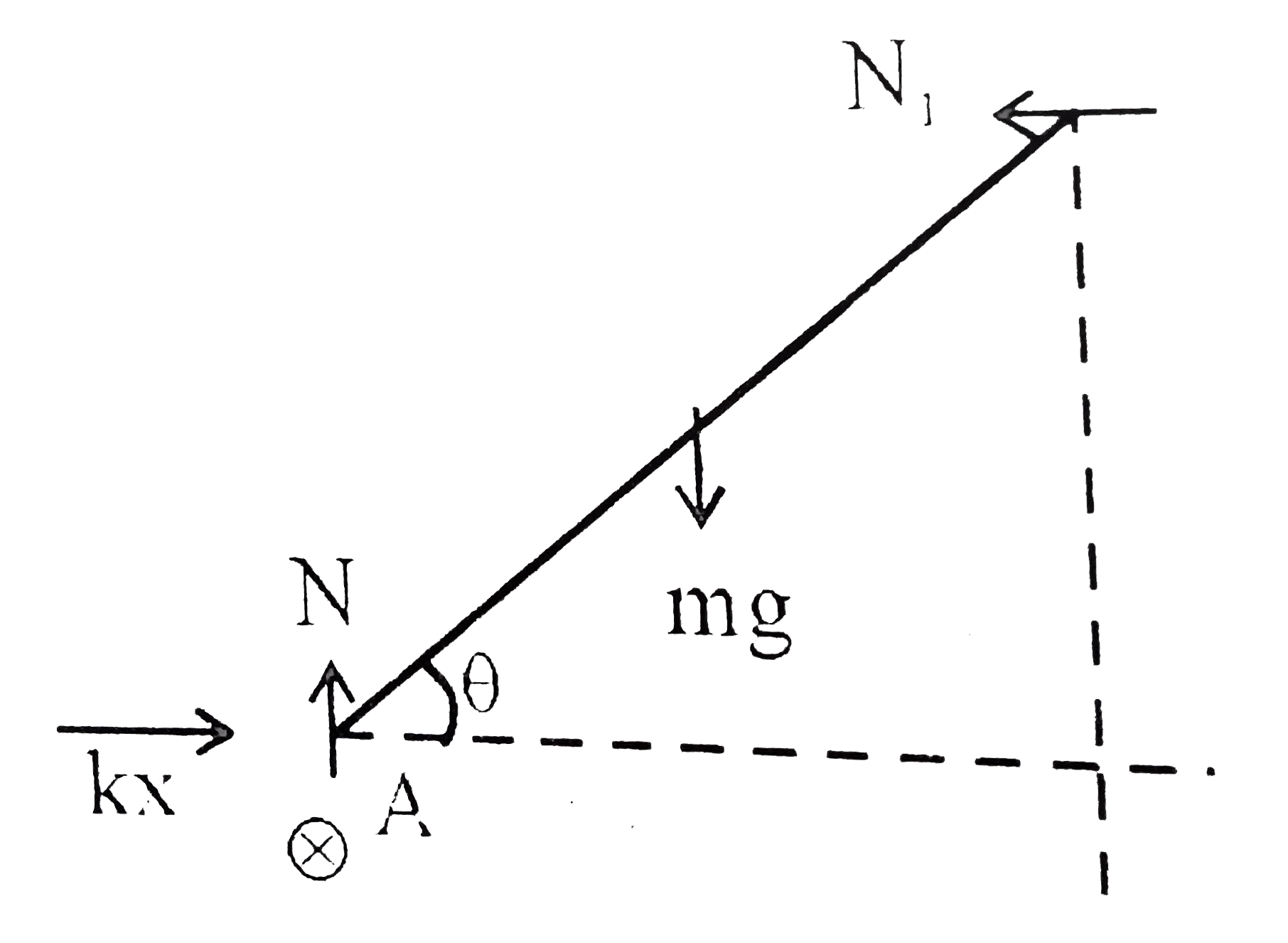
τA=0⇒mg,l2cosθ=N1lsinθ
N1=mgcotθ2
N1=kx⇒x=mgcotθ2k
x=mgcot60∘2,2mg1.(√3−1)=√3−14√3l
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
17 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
71 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
In the figure, block A is released from rest when the spring is its natural length for the block B of mass m to leave contact with the ground at some stage what should be the minimum mass of block A?
 .
.
View SolutionA thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

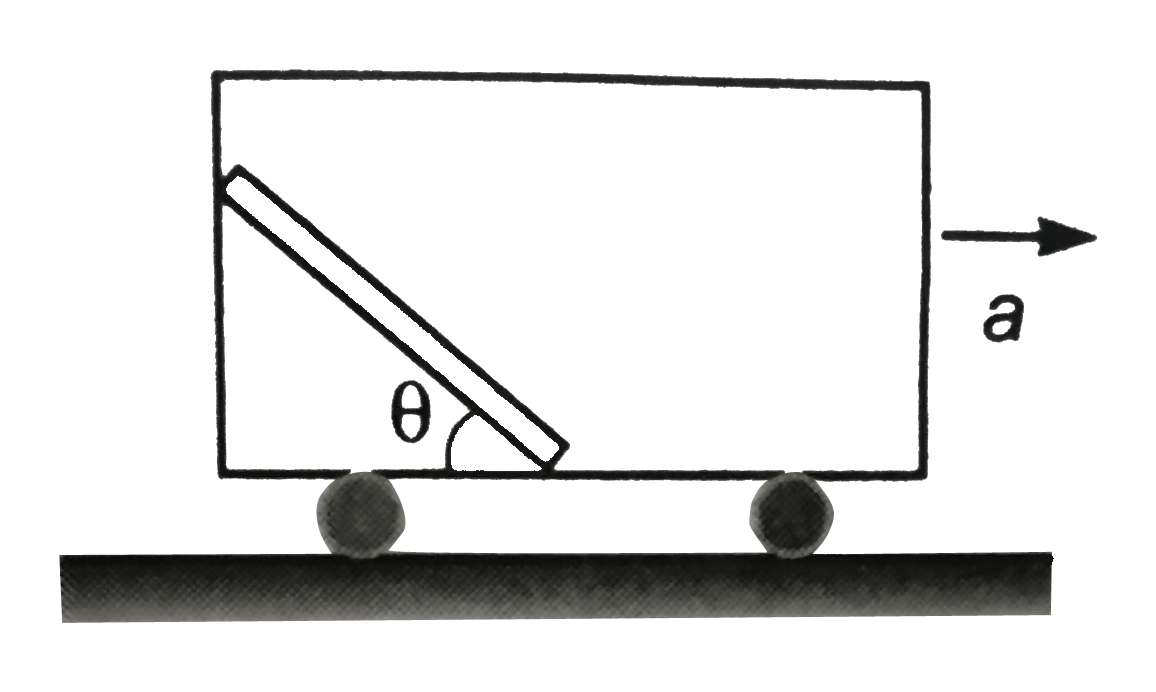
View SolutionA smooth rod length l is kept inside a trolley at an angle θ as shown in the figure. What should be the acceleration a of the trolley so that the rod remain in equilibrium with respect to it?
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is

View SolutionA uniform rod is placed vertically on a smooth surface and then released . Then,
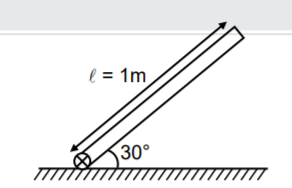
View SolutionA rod of length 1 m is released from rest as shown in the figure below: If ω of rod is √n at the moment it hits the ground, then find n.
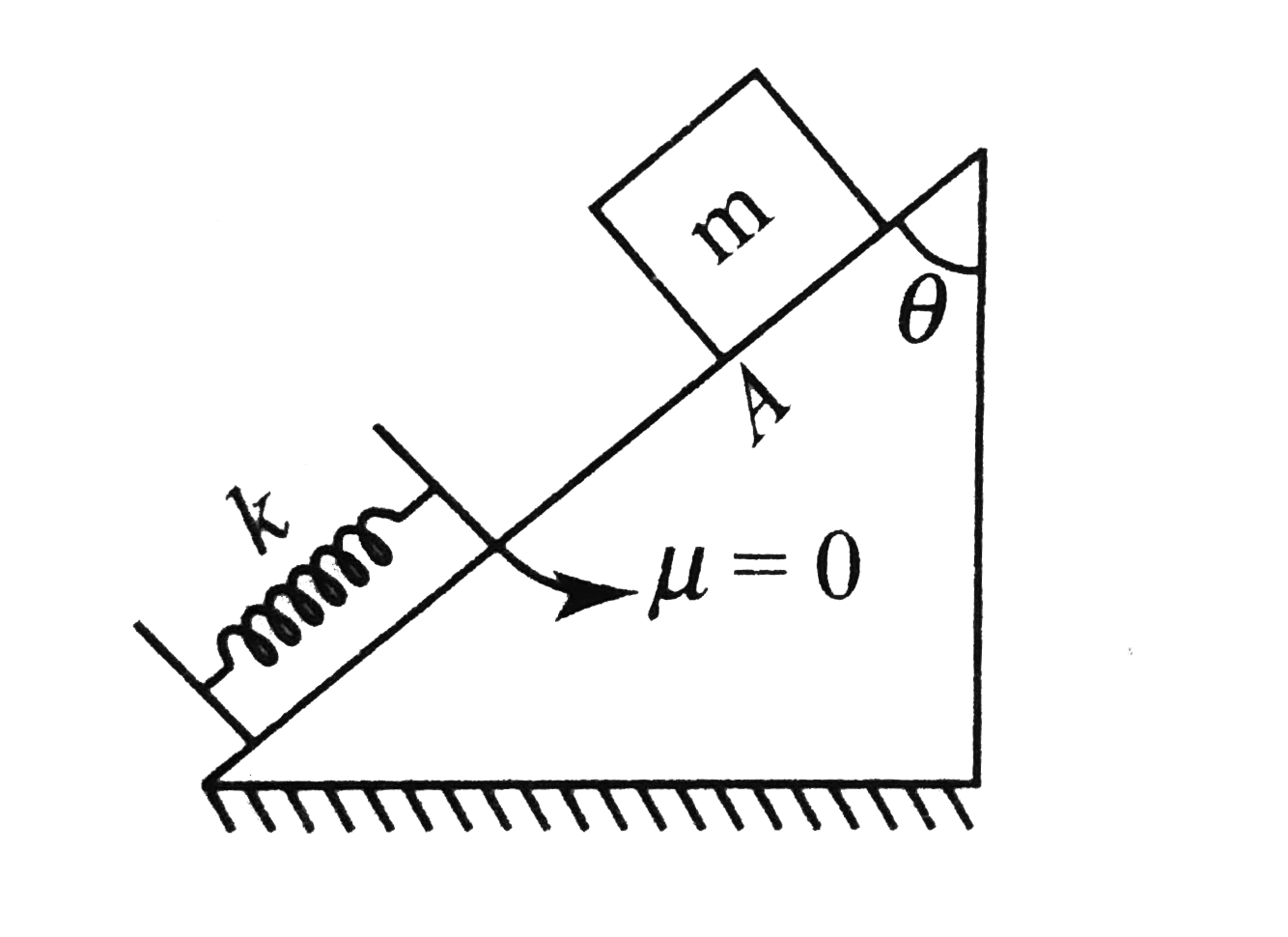
View SolutionA block of mass m is released from rest at point A. The compression in spring (force constant k) when the speed of block is maximum is found to be nmgcosθ4k. What should be the value of n?
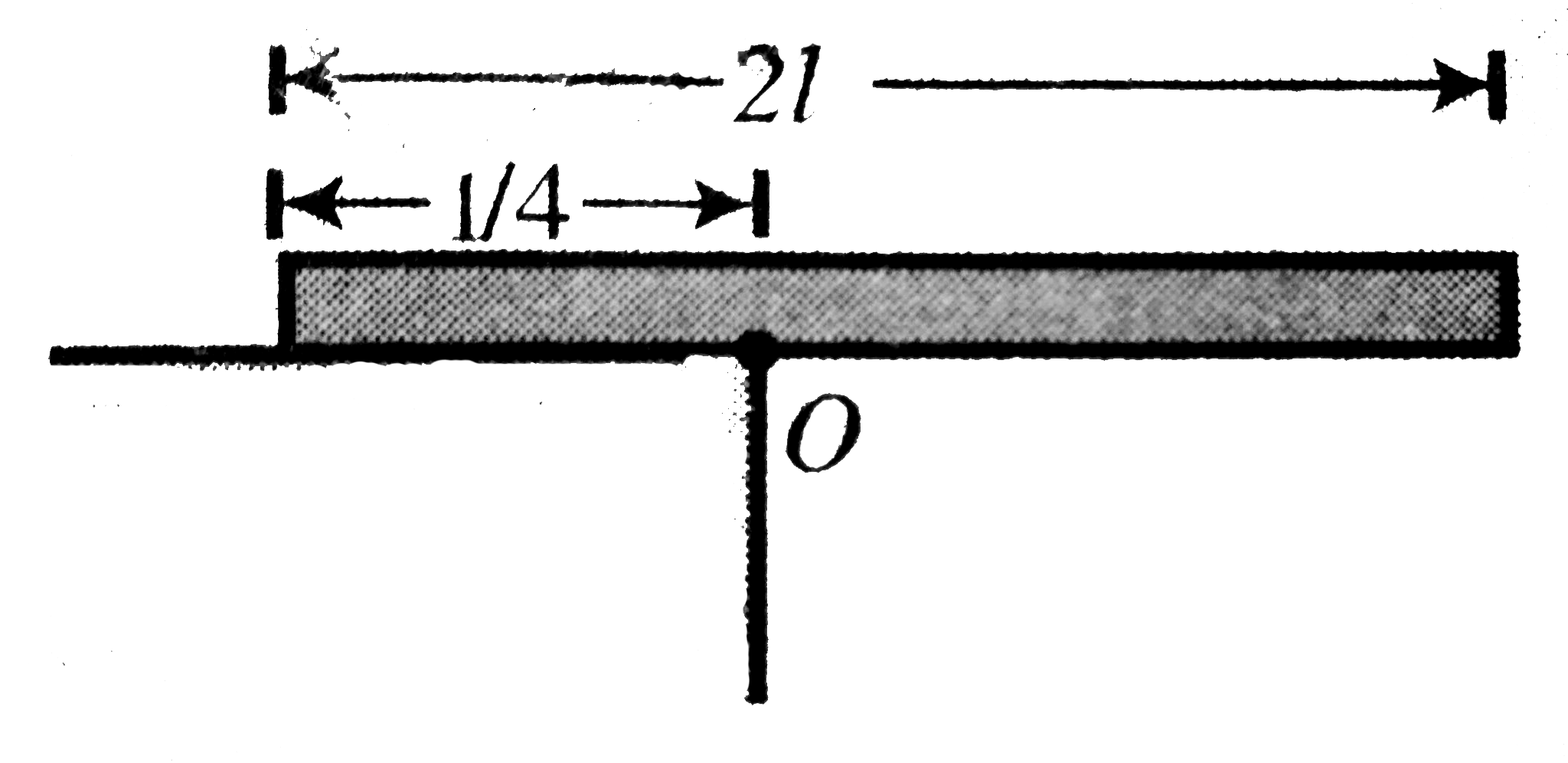
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
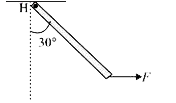
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
View Solution
