The length of a string attached to two rigid supports is 40 cm. The maximum wavelength in cm of a stationary wave produced on it is :
20
80
40
120
The correct Answer is:B
As the string is tied between two rigid supports hence there will be nodes at both ends. The longest wavelength for nodes at both ends will be the one
l=λ2⇒λ=2l
λlongest=2×40=80cm.
_E01_149_S01.png)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[B]42videos
WAVES AND OSCILLATIONS
- BOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[B]13videos
WAVES AND OSCILLATIONS
- BOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)51videos
SEMICONDUCTORS
Similar Questions
Length of a string tied to two rigid support is 40cm. Maximum length (wavelength in cm) of a stationary wave produced on it is
View Solution(a) A string of length L is stretched between two rigid supports. It is plucked at the centre. What type of wave is formed in it? What is its frequency?
(b) Obtain expressions for the frequency of higher harmonics of vibrations of a stretched string,
(c) State the laws of vibrating string-View Solution
Knowledge Check
- Question 1 - Select One
A second harmonic has to be generated in a string of length l stretched between two rigid supports. The point where the string has to be plucked and touched are
APlucked at L4 and touch at L2BPlucked at L4 and touch at 3L2CPlucked at L2 and touch at L2DPlucked at L2 and touch at 3L4 - Question 2 - Select One
One end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
Ay(t)=Asin(2πx)6cos(50πt)3By(t)=Asin(πx)3cos(100πt)3Cy(t)=Asin(5πx)6cos(255πt)3Dy(t)=Asin(5πx)2cos250πt
A stretched string is fixed at both its ends. Three possible wavelengths of stationary wave patterns that can be set up in the string are 90 cm, 60 cm and 45 cm. the length of the string may be
View SolutionA block M hangs vertically at the bottom end of a uniform rope of constant mass per unit length. The top end of the rope is attached to a fixed rigid support at O. A transverse wave pulse (Pulse 1) of wavelength λ0 is produced at point O on the rope. The pulse takes time TOA to reach point A. If the wave pulse of wavelength λ0 is produced at point A (Pulse 2) without disturbing the position of M it takes time TAO to reach point O. Which of the following options is/are correct?
 View Solution
View SolutionTwo masses of 10kg and 5kg are suspended from a rigid support as shown in figure. The system is pulled down with a force of 150N attached to the lower mass. The string attached to the support breaks and the system accelerates downwards
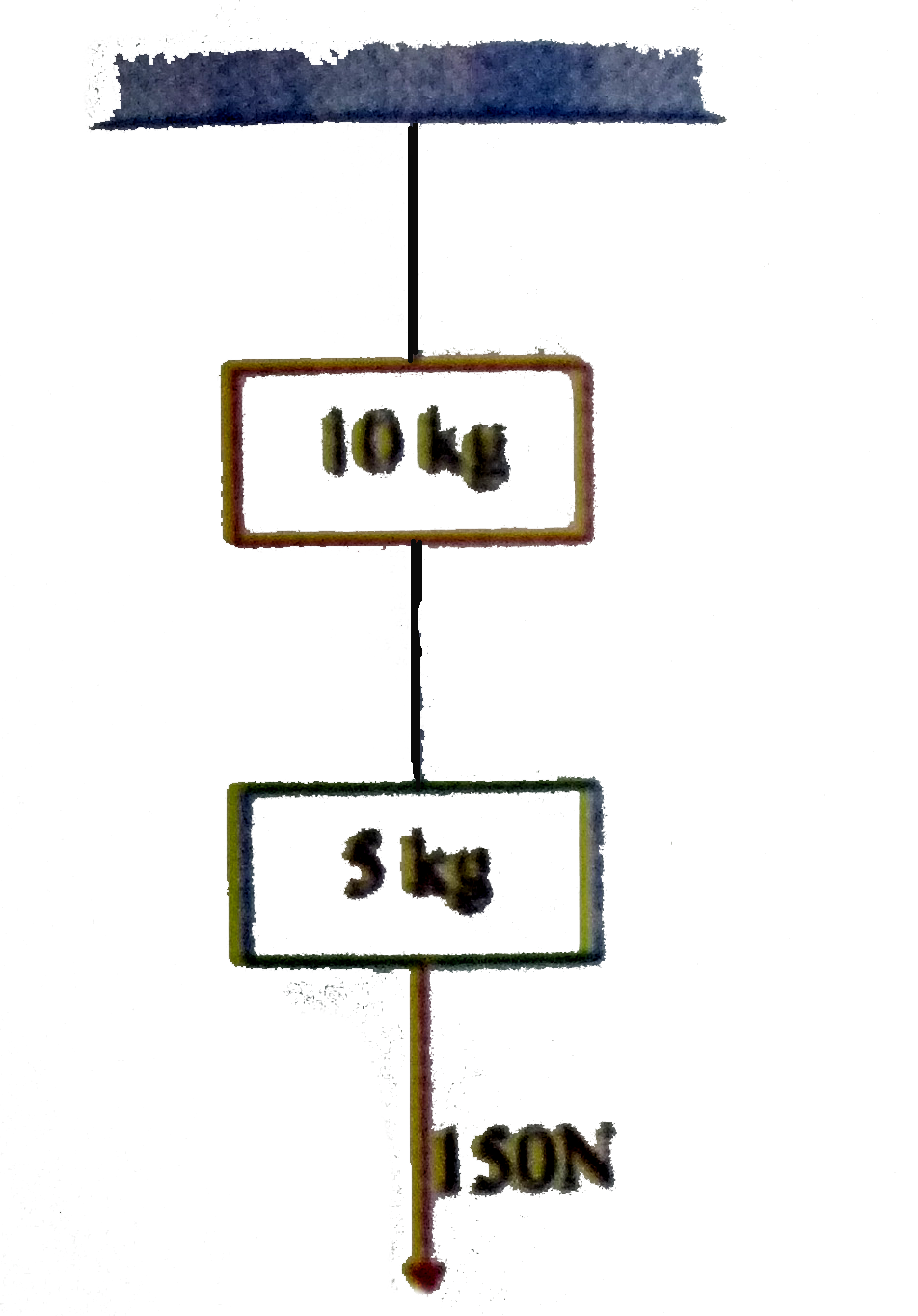
In case the force continues to act. what will be the tension acting between the two masses ? .View SolutionTwo masses of 10kg and 5kg are suspended from a rigid support as shown in figure. The system is pulled down with a force of 150N attached to the lower mass. The string attached to the support breaks and the system accelerates downwards
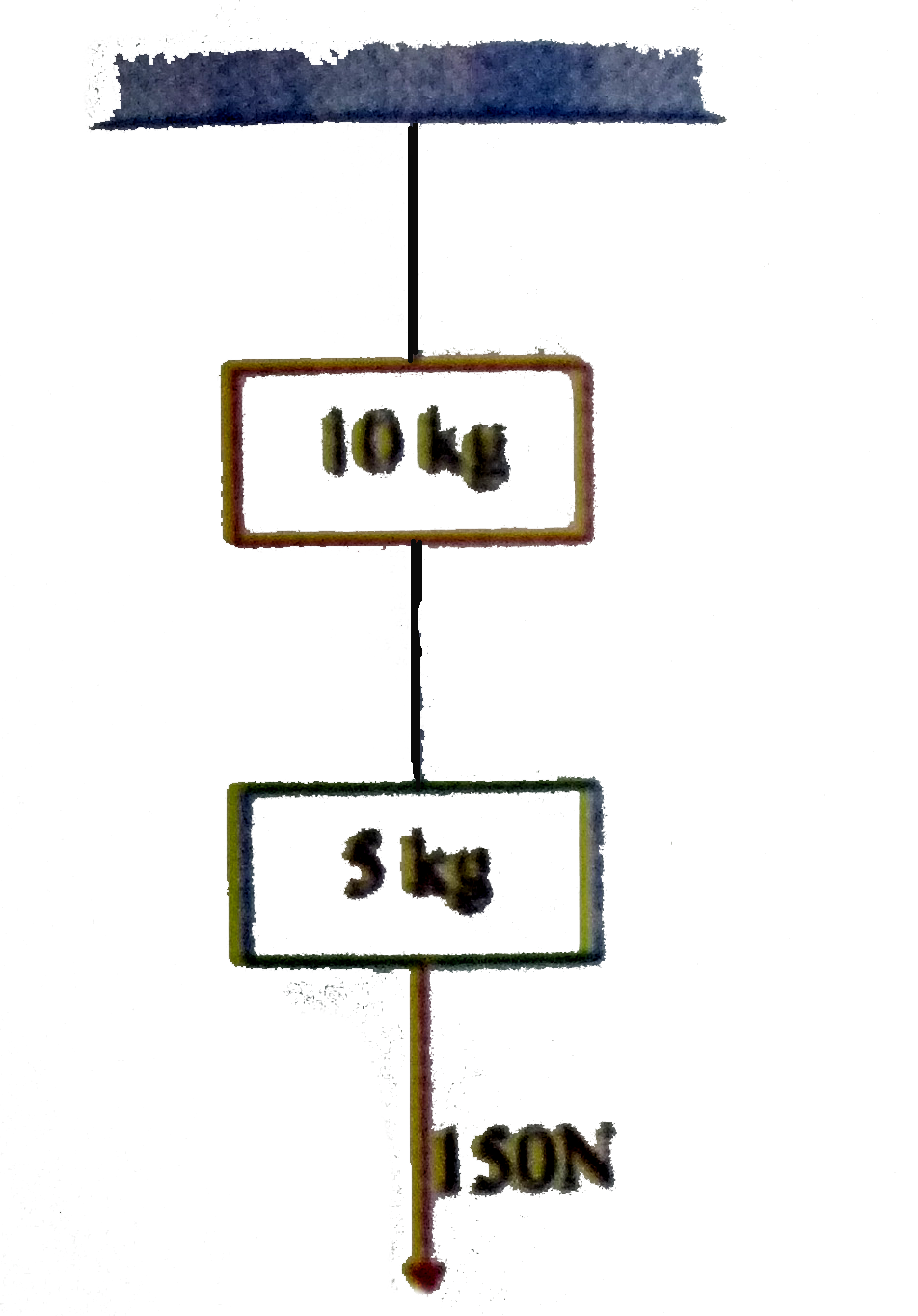
In case the force continues to act. what will be the tension acting between the two masses ? .View SolutionA steel wire of length 50√3cm is connected to an aluminium wire of length 60cm and stretched between two fixed supports. The tension produced is 104N, if the cross section area of each wire is 1mm2. If a transverse wave is set up in the wire, find the lowest frequency for which standing waves with node at the joint are produced . (density of aluminimum =2.6gm/cm3 and density of steel =7.8gm/cm3).
View SolutionA standing wave of time period T is set up in a string clamped between two rigid supports, At t=0 antinode is at its maximum displacement 2A.
View Solution
