Length of a string tied to two rigid support is 40cm. Maximum length (wavelength in cm) of a stationary wave produced on it is
20
80
40
120
The correct Answer is:B
To solve the problem of finding the maximum wavelength of a stationary wave produced on a string tied to two rigid supports, we can follow these steps:
1. Understand the Setup: The string is tied between two rigid supports, creating a fixed length. The length of the string (L) is given as 40 cm.
2. Identify the Wave Characteristics: In a stationary wave, nodes and antinodes are formed. The maximum wavelength occurs when there is one antinode in the middle of the string.
3. Determine the Relationship Between Length and Wavelength: For a string fixed at both ends, the relationship between the length of the string (L) and the wavelength (λ) is given by:
L=λ2
This means that the length of the string is half of the wavelength when there is one antinode.
4. Calculate the Wavelength: Rearranging the formula gives us:
λ=2L
Substituting the given length of the string:
λ=2×40cm=80cm
5. Conclusion: The maximum wavelength of the stationary wave produced on the string is 80 cm.
Final Answer:
The maximum wavelength of the stationary wave produced on the string is 80 cm.
---
L=λ2
This means that the length of the string is half of the wavelength when there is one antinode.
λ=2L
Substituting the given length of the string:
λ=2×40cm=80cm
The maximum wavelength of the stationary wave produced on the string is 80 cm.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 232videos
WAVE MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (MUTIPLE CORRECT TYPE)20videos
WAVE MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - LEVEL-241videos
WAVE MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B10videos
UNITS, MEASUREMENTS & ERRORS
- BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE54videos
WORK ENERGY AND POWER
Similar Questions
(a) A string of length L is stretched between two rigid supports. It is plucked at the centre. What type of wave is formed in it? What is its frequency?
(b) Obtain expressions for the frequency of higher harmonics of vibrations of a stretched string,
(c) State the laws of vibrating string-View SolutionA stretched string is fixed at both its ends. Three possible wavelengths of stationary wave patterns that can be set up in the string are 90 cm, 60 cm and 45 cm. the length of the string may be
View Solution
Knowledge Check
- Question 1 - Select One
A second harmonic has to be generated in a string of length l stretched between two rigid supports. The point where the string has to be plucked and touched are
APlucked at L4 and touch at L2BPlucked at L4 and touch at 3L2CPlucked at L2 and touch at L2DPlucked at L2 and touch at 3L4 - Question 2 - Select One
One end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
Ay(t)=Asin(2πx)6cos(50πt)3By(t)=Asin(πx)3cos(100πt)3Cy(t)=Asin(5πx)6cos(255πt)3Dy(t)=Asin(5πx)2cos250πt
A string is fixed between two rigid support. Mass per unit length of the string is lambda. Now the tension in the wire is decreased by 19%. The percentage decrease in frequency will be
View SolutionA string is tied at two rigid supports . A pulse is generated on the string as shown in figure . Minimum time after which string will regain its shape as shown in figure ( Neglect the time during reflection )
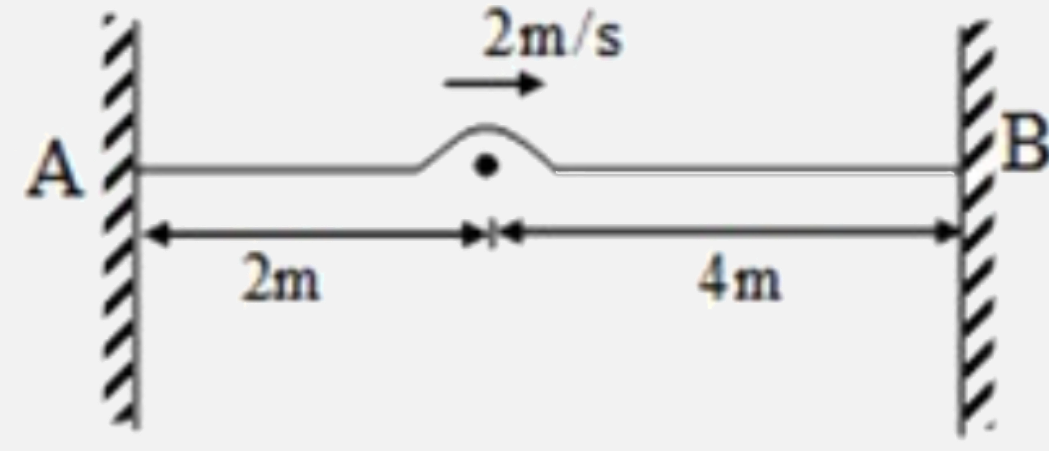 View Solution
View SolutionA thick uniform rope of length L is hanging from a rigid support. A transverse wave of wavelength λ0 is set up in the middle of the rope. The wavelength of the wave as it reaches the top most point is
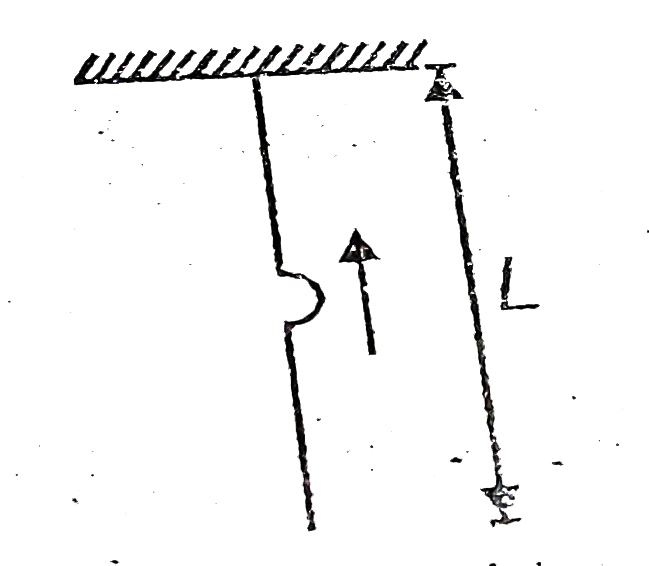 View Solution
View SolutionA 1m long rope, having a mass of 40g, is fixed at one end and is tied to a light string at the other end. The tension in the string in 400N. Find the wavelength in second overtone (in cm).
View SolutionThe wavelength of waves produced on the surface of water is 20 cm. If the wave velocity is 24 ms−1, calculate
The number of waves produced in one second andView SolutionAn harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubledView Solution
