Question

The lens governing the behavior of the rays namely rectilinear propagation laws of reflection and refraction can be summarised in one fundamental law known as Fermat's principle. According to this principle a ray of light travels from one point to another such that the time taken is at a stationary value (maximum or minimum).
if c is the velocity of light in a vacuum the velocity in a medium of refractive index ${\displaystyle \mu }$ is ${\displaystyle \frac{c}{\mu }}$ hence time taken to travel a distance ${\displaystyle l}$ is ${\displaystyle \frac{\mu l}{c}}$ if the light passes through a number of media, the total time taken is ${\displaystyle \left(\frac{1}{c}\right)\sum \mu l}$ or ${\displaystyle \frac{1}{c}\int \mu dl}$ if refractive index varies continuously. Now ${\displaystyle \sum \mu l}$ is the total path, so that fermat's principle states that the path of a ray is such that the optical path in at a stationary value. this principle is obviously in agreement with the fact that the ray are straight lines i a homogenous isotropic medium. it is found that it also agrees with the classical laws of reflection and refraction.
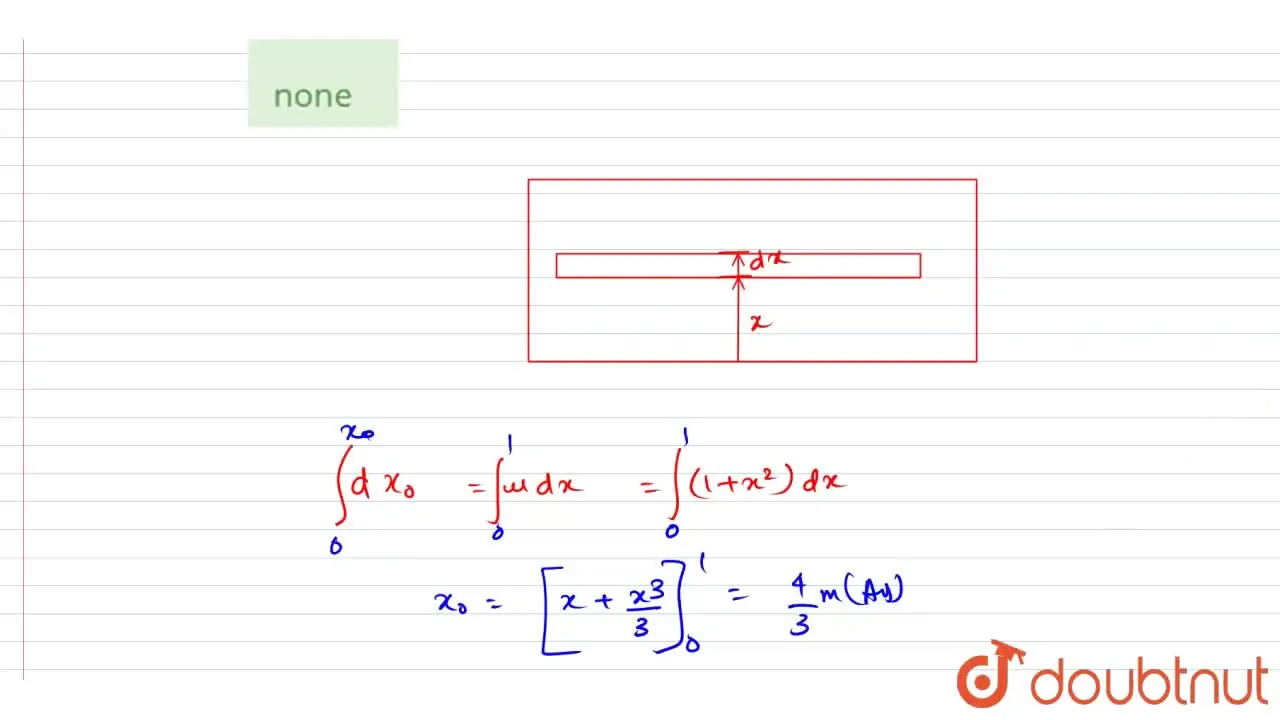
Q. If refractive index of a slab varies as ${\displaystyle \mu =1+x^2}$ where x is measured from one end then optical path length of a slab of thickness 1 m is

Options

A. `(4)/(3)m`
B. `(3)/(4)m`
C. `1m`
D. none

Answer

A

Explanation

To find the optical path length of a slab of thickness 1 m where the refractive index varies as $$\mu =1+x^2$$, we can follow these steps:

Step 1: Understand the Optical Path Length
The optical path length (OPL) is defined as the product of the refractive index (\( \mu \)) and the physical path length (\( dx \)). For a small element of thickness \( dx \), the optical path length can be expressed as:
\( dOPL = \mu \, dx \)

Step 2: Substitute the Refractive Index
Given that the refractive index varies with \( x \) as \( \mu = 1 + x^2 \), we can substitute this into the equation for optical path length:
\( dOPL = (1 + x^2) \, dx \)

Step 3: Set Up the Integral
To find the total optical path length for the entire slab of thickness 1 m, we need to integrate \( dOPL \) from \( x = 0 \) to \( x = 1 \):
\( OPL = \int_{0}^{1} (1 + x^2) \, dx \)

Step 4: Perform the Integration
Now, we can evaluate the integral:
\( OPL = \int_{0}^{1} 1 \, dx + \int_{0}^{1} x^2 \, dx \)
Calculating each part:
1. The first integral:
\( \int_{0}^{1} 1 \, dx = (x)_{0}^{1} = 1 - 0 = 1 \)
2. The second integral:
\( \int_{0}^{1} x^2 \, dx = \left(\frac{x^3}{3}\right)_{0}^{1} = \frac{1^3}{3} - \frac{0^3}{3} = \frac{1}{3} \)

Step 5: Combine the Results
Now, we can combine the results of the integrals:
\( OPL = 1 + \frac{1}{3} = \frac{3}{3} + \frac{1}{3} = \frac{4}{3} \)

Final Answer
Thus, the optical path length of the slab of thickness 1 m is:
\( \text{Optical Path Length} = \frac{4}{3} \text{ m} \)