Two identical monochromaticlight sources A & B intensity 10−15W/m2 produce wavelength of light 4000√3Å A glass of thickness 3mm is placed in the path of the ray as shown in figure the glass has a varible refractive index n=1+√x where x (in mm) is distance of plate from left to right calculate total intensity at focal points F of the lens.
_E01_100_Q01.png)
The correct Answer is:4×10−15W/m2
I=10−15W/m2,λ=4000√3Å,t=3mm
The path difference due to glass plate 3mm. ltbr> Path difference =∫ds=∫3mm0(n−1)dx
∫30(1+√x−1)dx=23x3/2=2√3mm
∴ Phase difference
=2π4000√3×10−10×2√3×10−3=π×107−3
∴2πn=104×π
At point I there is point of maxima n=5×103
∴ intensity =I+I+2√I×√Icos104π
=4I=4×10−15W/m2
_E01_100_S01.png)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 5 A (Previous Years Questions)17videos
WAVE OPTICS
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 5 B (Previous Years Questions)19videos
WAVE OPTICS
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 4 A (Conceptual subjective Exercise)9videos
WAVE OPTICS
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
There is an insect a cabin eying towards thick glass plate P1, Insect sees the images of light source acrss the glass plate P1 outside tha chain. Cabin is made of thick glass plates of refractive index μ=32 and thickness 3cm. Insect is eying from the middle of the cabin as shown in figure. (glass plates are partially reflective and consider only paraxial rays)
At what distance (from eye of insect) will the eye see the image ?View SolutionA ray of light is icncident at anangle of 60∘ on one face of a ractangular glass slab of thickness 2√3 mm refractive index √3 , Calculate the lateral shift produced in mm.
View SolutionIn a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
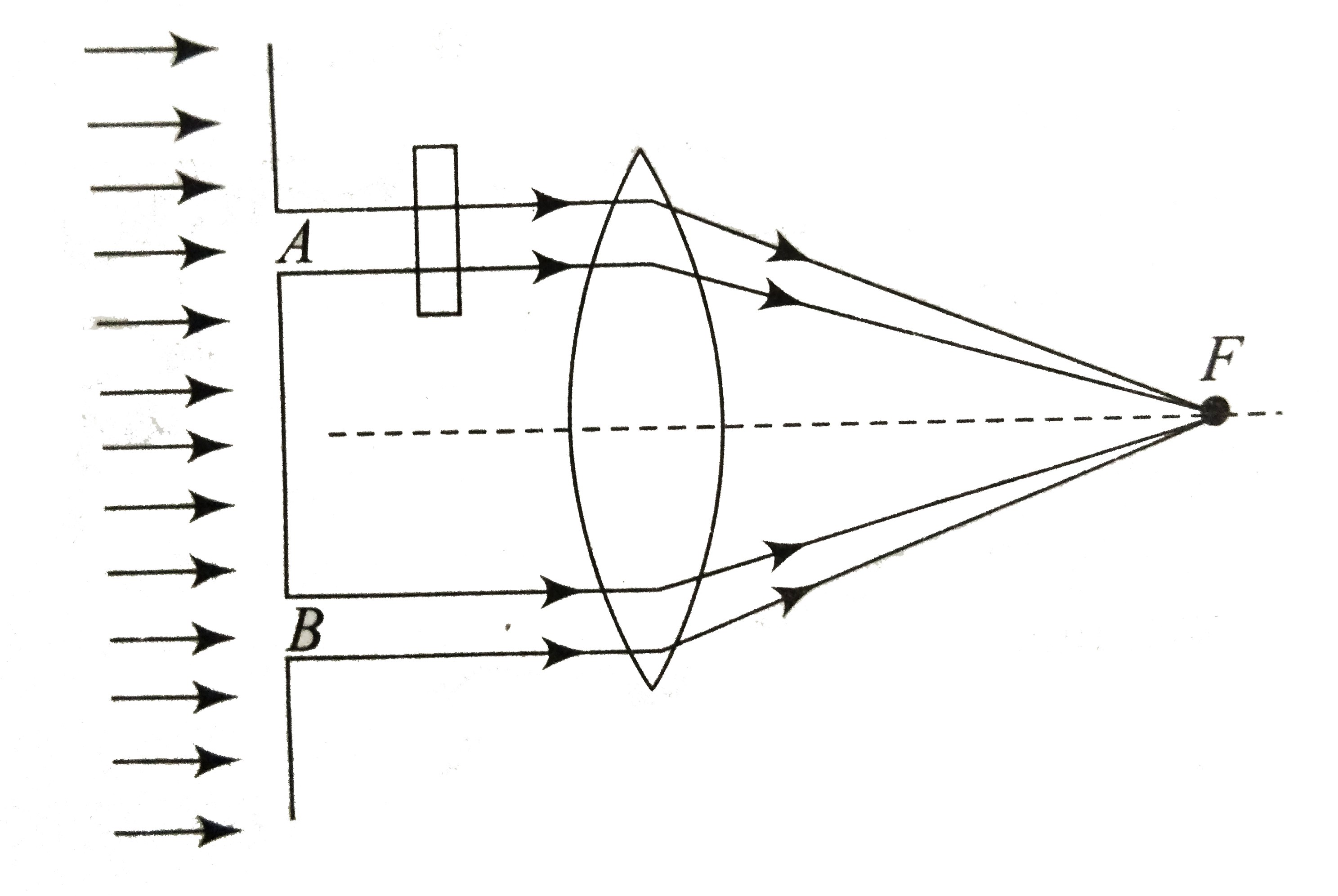View SolutionA ray of light travelling in air is incident at grazing incidence on a slab with variable refractive index, n (y)=[ky3/2+1]1/2 where k=1m−3/2 and follows path as shown in the figure. What is the total deviation produced by slab when the ray comes out.
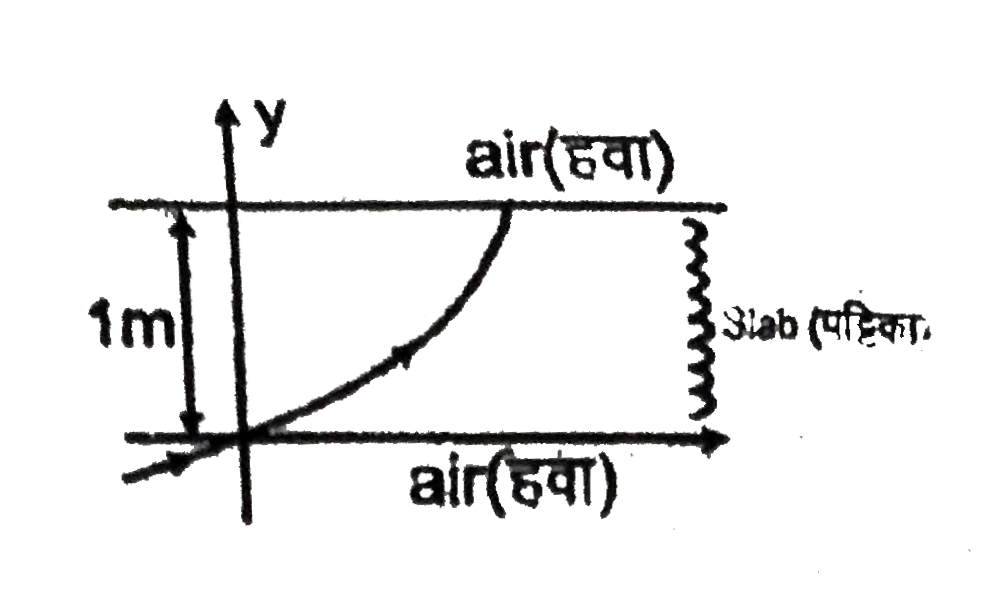View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
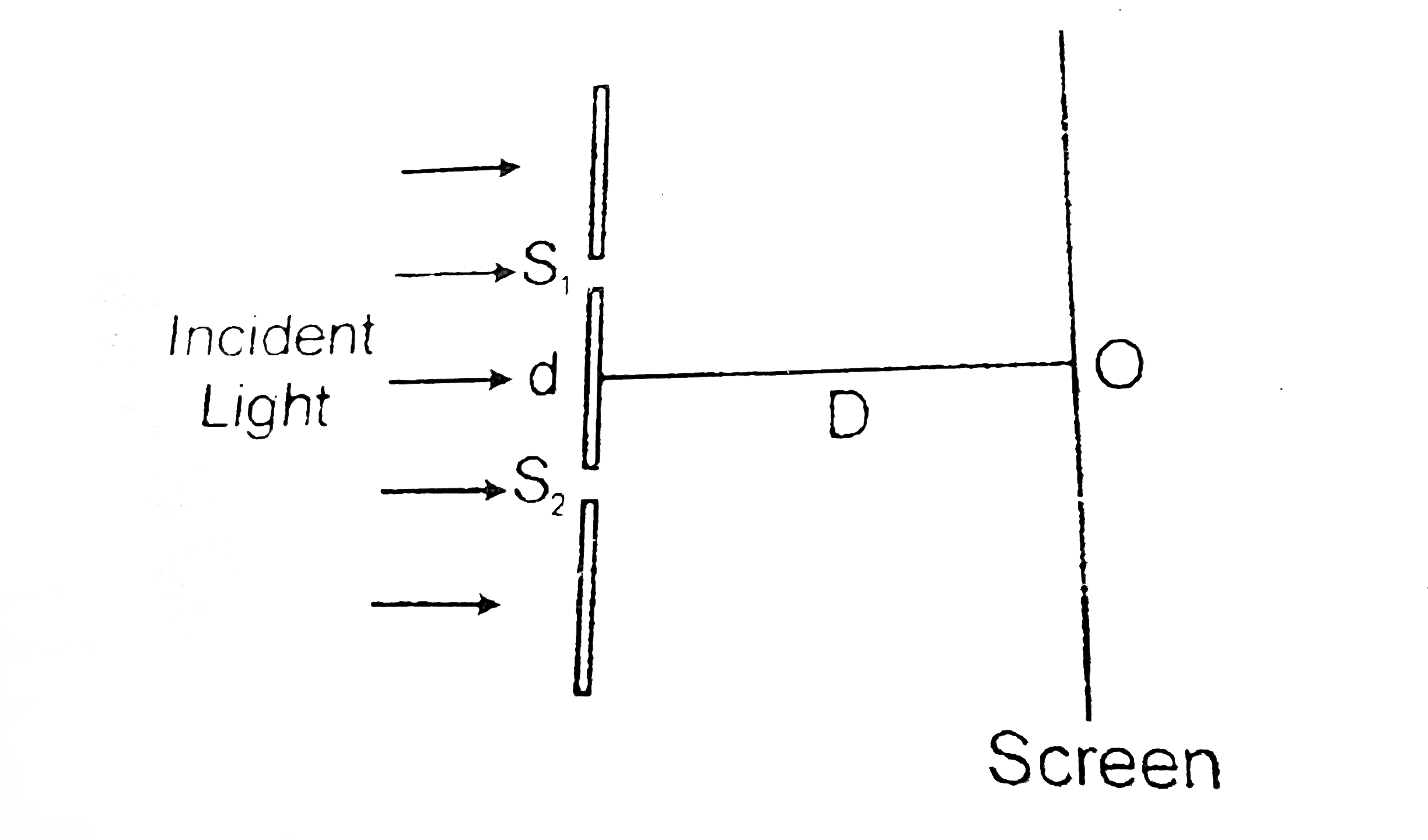
After placing the film of slit S1, the intensity at point O screen is :View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
After placing the film of slit S1, the intensity at point O screen is :View SolutionIn a Young's double slit experiment, a parallel beam containing wavelengths λ1=4000Å and λ2=5600Å is incident at an angle ϕ=30∘ on a diaphragm having narrow slits at separation d=2mm. The screen is placed at a distance D =40 cm from the slits. a mica slab of thickness t=5mm is placed in front of one of the slits and whole of the apparatus is submerged in water. if the central bright fringe is observed at C, determine.
(i) The refractive index of the slab
(ii) The distance of first black line from C
both wavelength are in air. take μw=43View SolutionA monochromatic light of λ=500nm is incident on two identical slits separated by a distance of 5×10−4m. The interference pattern is seen on a screen placed at a distance of 1m from the plane of slits. A thin glass plate of thickness 1.5×10−6m and refractive index μ=1.5 is placed between one of the slits and the screen. Find the intensity at the center of the screen if the intensity is I0 in the absence of the plate. Also find the lateral shift of the central maxima and number of fringes crossed through center.
View SolutionIn the YDSE, the monochromatic source of wavelength λ is placed at a distance d2 from the central axis (as shown in the figure), where d is the separation between the two slits S1andS2 .
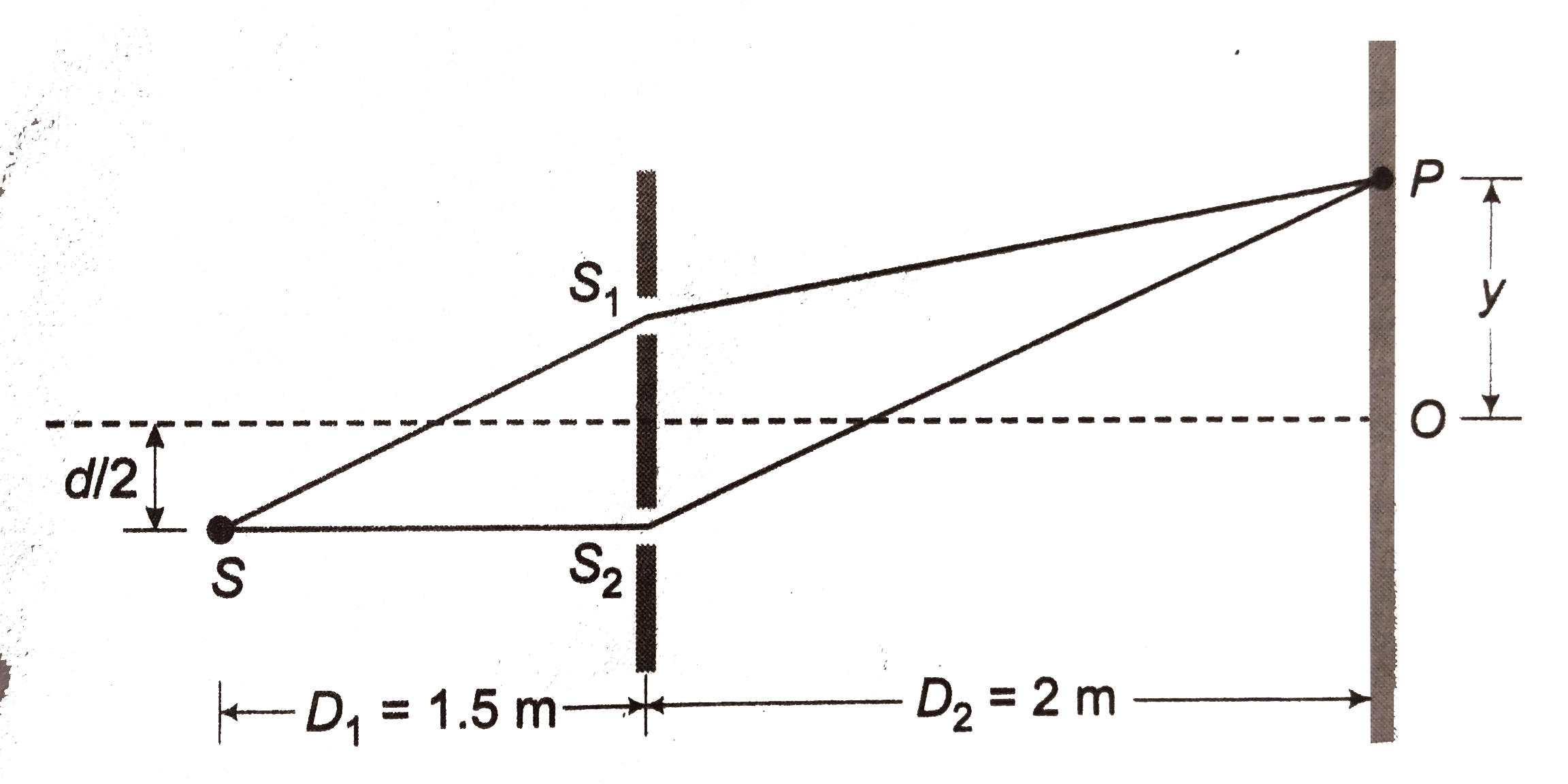
(a)Find the position of the central maxima.
(b) Find the order of interference formed at O.
(c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes μ=1.5 to be placed in front of S2 so that intensity at O becomes 34th of the maximum intensity.
(Take λ=6000Å,d=6mm.)View SolutionA convex lens of focal length f1 is placed in front of a luminous point object. The separation between the object and the lens is 3f1 . A glass slab of thikness t is placed between the object and the lens. A real image of the object is formed at the shortest possible distance from the object.
a. Find the refractive index of the slab.
b. If a concave lens of very large focal length f2 is placed in contact with the convex lens, find the shifting of the image.View Solution