Let S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
λ/θ
λθ
2λ/θ
λ/2θ
The correct Answer is:A
_E01_034_S01.png)
As distance between S1 & S2 is very much medium. And equal to 'd' so the angle made at 'P' is very much small
∴ angle =ArcD⇒θ=dD
∴ fringe width =λDd=λθ(∵dD=θ)
Topper's Solved these Questions
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 2 (Brain Teasures)
Explore 22 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 3 (Miscellaneous type Questions)
Explore 27 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Example 15
Explore 1 Video
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
Let S1andS2 be the two slits in Young's double slit experiment. If central maxima is observed at P and angle S1PS2=θ, (θ is small) find the y-coordinates of the 3rd minima assuming the origin at the central maxima. (λ = wavelength of monochromatic light used).
View SolutionIf the width of the slit S in Young's double slit experiment is gradually increased

View SolutionIn Young.s double slit experiment the band width is minimum for the colour
View SolutionIn the Young’s double slit experiment, for which colour the fringe width is least
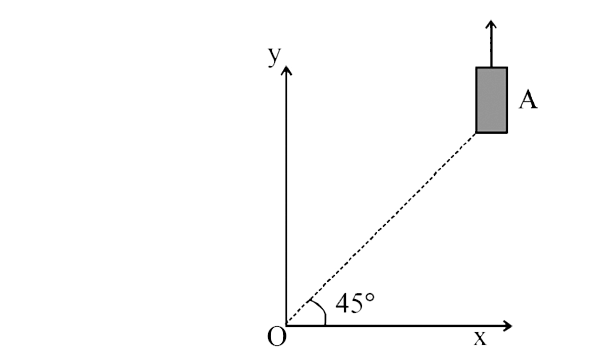
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
View SolutionIf the separation between slits in Young’s double slit experiment is reduced to 13 rd, the fringe width becomes n times. The value of n
View SolutionIn Young's double slit experiment, the distance between two slits is made three times then the fringe width will becomes
View SolutionIn a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
View SolutionIn a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
View SolutionIn a Young's double slit experiment, I0 is the intensity at the central maximum and β is the fringe width. The intensity at a point P distant x from the centre will be
View Solution

