_S01_033_Q01.png)
In a typical young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity v=1 mm per second towards the screen, then the instantaneous velocity of central maxima is given as α×10−βcm/s upward in scientific notation find the value of α+β
_S01_033_S01.png)
The central maxima dyD=√d2+x2−x=x[1+d22x2]−x=d22x
y=Dd2x⇒dydt=−Dd2x2(dxdt)=(1×0.012×0.5×0.5)×(0.001)=0.02mm/s
⇒y=2×10−3cm/s⇒α+β=5
Topper's Solved these Questions
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 1 (Check your Grasp)
75 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Brain Teasures)
22 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Example 14
1 Video
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
In the youngs double slit experiment ,the slit sepration is 1mm ,the distance between source and screen is 1m ,wavelength of light used is 6500 angstrom.Find the distance between fifth maxima and third minima in (mm)?
View SolutionIn Young.s double slit experiment with monochromatic source of light of wavelength 6000A2, if the path difference at a point on the screen is 6×10−6m, the number of the bright band formed at that point is
View Solution
Knowledge Check
In Young's double slit experiment, the slits are horizontal. The intensity at a point P as shown in figure is 34I0,whereI0 is the maximum intensity.
Then the value of θ is,
(Given the distance between the two slits S1 and S2 is 2λ)
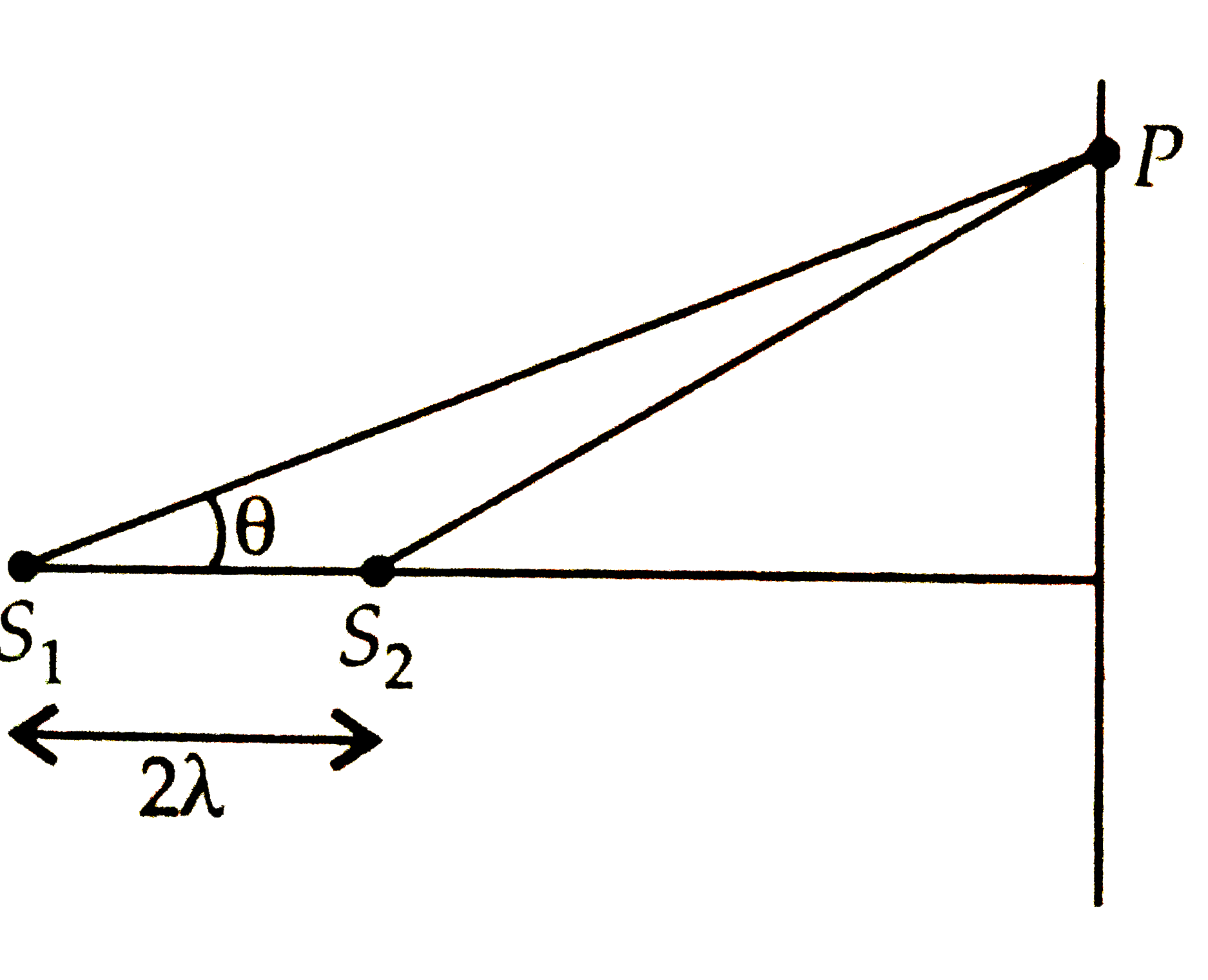 Acos−1(112)Bsin−1(112)Ctan−1(112)Dsin−1(35)
Acos−1(112)Bsin−1(112)Ctan−1(112)Dsin−1(35)
In a Young's double slit experiment, slits are seperated by a distance d and screen is at distance D, (D>>d) from slit plane. If light source of wavelength λ(λ<<d) is used. The minimum distance from central point on the screen where intensity is one fourth of the maximum is Dλnd. Find the value of n.
View Solution(a) In young.s double slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is move by 5×10−2 m towards the slits, the change in the fringe width is 3×10−5 m. If the distance between the two slits is 10−3 m, calculate wavelength of the light used.
(b) What is meant by .Chromatic aberration. ? A thin convex lens of focal length 30 cm and made of flint glass (dispersive power= 0.03) is kept in contact with a thin cancave lens of focal length 20 cm and made of crown glass. Calculate the dispersive power of crown glass if the above said combination acts as an achromatic doublet.
View SolutionIn Young's double slit experiment the point source is placed slightly off the central axis as shown in figure. The plane of slits (S1,S2) and screen are separated by a distance of 2m. The separation between the slits is 10 mm. The position of the slit above the axis is 1mm. if the wavelength λ=4000Å in the above arrangement

The thickness of the film in the above case is
View SolutionIn a Young’s double slit experiment a monochromatic light whose wavelength is l strikes on the slits, separated by distance d, as shown in the figure. Refractive index of the medium between slits and screen varies with time t as n = n0 + kt. Here n0 and k are positive constants. Position of any point P on screen is measure by its y-coordinate as shown.
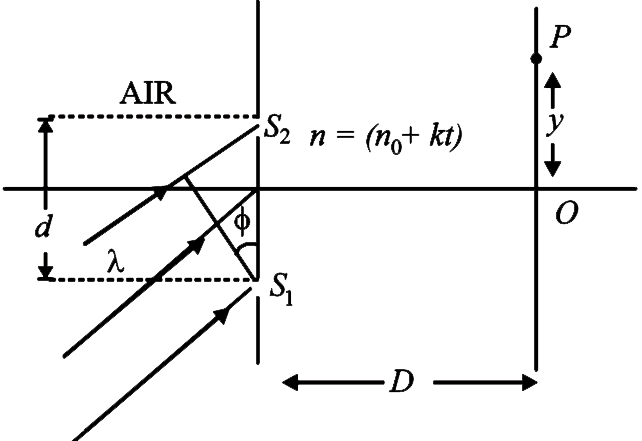
If a glass plate of small thickness b is placed in front of S1. How should its refractive index vary with time so that central maxima is formed at O.
View SolutionIn young's double slit experiment, the screen is kept 1.6m from the slits. The coherent sources are 0.032 cm apart and fringes are observed on the screen. It is found that with a certain monochromatic source of light, the fourth bright fringe is situated at a distance of 1.06 cm from the central fringe. The wavelength of the light used is
View SolutionFrom the given figure, find :
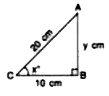
x∘
View SolutionIn Young's double slit experiment the two slits 0.12 mm apart are illuminated by monochromatic light of wavelength 420 nm. The screen is 1.0 m away from the slits .
(a) Find the distance of the second (i) bright fringe , (ii) dark fringe from the central maximum .
(b) How will the fringe pattern change if the screen is moved away from the slits ?
View Solution