In a Young’s double slit experiment a monochromatic light whose wavelength is l strikes on the slits, separated by distance d, as shown in the figure. Refractive index of the medium between slits and screen varies with time t as n = n0 + kt. Here n0 and k are positive constants. Position of any point P on screen is measure by its y-coordinate as shown.
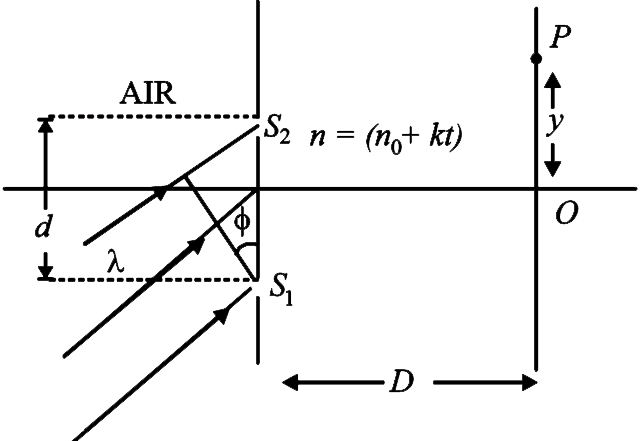
If a glass plate of small thickness b is placed in front of S1. How should its refractive index vary with time so that central maxima is formed at O.
(a) S1P−S2P=dyD
Δx=(n0+kt)dyD−dsinϕ=0
For central maxima.
∴y=Dsinϕn0+kty-coordinates of central maximum
(b) dydt=−kDsinϕ(n0+kt)2= velocity of central maximum
(c) For central maxima to be formed at O
n'(nn'−1)P=dsinϕ Here n'=n0+kt, n= refractive index of plate
n=n0+kt+dsinϕP
Similar Questions
In Young's double slit experiment parallel monochromatic light is incident on both the slits at an angle as shown in the figure. To obtain the central maxima at on the screen we can
View SolutionIn the Young's double slit experiment using a monochromatic light of wavelength λ, the path difference (in terms of an integer n) corresponding to any point having half the peak
View Solution
Knowledge Check
In a Young's double slit experiment, (slit distance d) monochromatic light of wavelength λ is used and the fringe pattern observed at a distance D from the slits. The angular position of the bright fringes are
Asin−1(Nλd)Bsin−1⎛⎜ ⎜⎝(N+12)λd⎞⎟ ⎟⎠Csin−1(NλD)Dsin−1⎛⎜ ⎜⎝(N+12)λD⎞⎟ ⎟⎠
In the Young's double slit experiment using a monochromatic light of wavelength λ, the path difference (in terms of an integer n) corresponding to any point having half the peak
View SolutionA particle is placed on the top of a hemispherical shell of same mass. Shell is free to move on the smooth ground. If particle is given a given a gentle push and reaches to angular position q as shown in figure then for an observer fixed on a shell, ratio of reaction force exerted by shell to pseudo force (as observed from shell) acting on particle, is

View SolutionIn a Young’s double slit experiment, the separation of the two slits is doubled. To keep the same spacing of fringes, the distance D of the screen from the slits should be made
View SolutionYoung’s double slit experiment is performed with light of wavelength 550 nm . The separation between the slits is 1.10mm and screen is placed at distance of 1 m . What is the distance between the consecutive bright or dark fringes
View SolutionIn Young.s double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0.48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate :
Distance between the two slits.
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View Solution