Let S1andS2 be the two slits in Young's double slit experiment. If central maxima is observed at P and angle S1PS2=θ, (θ is small) find the y-coordinates of the 3rd minima assuming the origin at the central maxima. (λ = wavelength of monochromatic light used).
±2λθ
±5λ2θ
±52λθ
±2λθ
The correct Answer is:B
To find the y-coordinate of the third minima in Young's double slit experiment, we can follow these steps:
Step 1: Understand the condition for minima
In Young's double slit experiment, minima occur when the path difference between the light coming from the two slits is an odd multiple of half the wavelength, i.e.,
Δd=(m+12)λ
where m is an integer (0, 1, 2, ...). For the third minima, m=2:
Δd=(2+12)λ=52λ
Step 2: Relate path difference to geometry
The path difference Δd can also be expressed in terms of the angle θ and the distance between the slits d:
Δd=dsin(θ)
For small angles, we can use the approximation sin(θ)≈θ (in radians). Thus, we have:
Δd≈dθ
Step 3: Set up the equation for the third minima
From the previous steps, we can equate the two expressions for the path difference:
dθ=52λ
Step 4: Solve for θ
Rearranging the equation gives:
θ=5λ2d
Step 5: Find the y-coordinate
In the geometry of the setup, the y-coordinate of the minima can be expressed as:
y=Dtan(θ)
For small angles, tan(θ)≈θ. Thus,
y≈Dθ
Substituting the expression for θ:
y≈D(5λ2d)
This gives:
y=5Dλ2d
Step 6: Consider both directions for minima
Since minima can occur above and below the central maxima, the y-coordinates for the third minima are:
y=±5Dλ2d
Final Result
The y-coordinates of the third minima are:
y=5Dλ2dandy=−5Dλ2d
In Young's double slit experiment, minima occur when the path difference between the light coming from the two slits is an odd multiple of half the wavelength, i.e.,
Δd=(m+12)λ
where m is an integer (0, 1, 2, ...). For the third minima, m=2:
Δd=(2+12)λ=52λ
The path difference Δd can also be expressed in terms of the angle θ and the distance between the slits d:
Δd=dsin(θ)
For small angles, we can use the approximation sin(θ)≈θ (in radians). Thus, we have:
Δd≈dθ
From the previous steps, we can equate the two expressions for the path difference:
dθ=52λ
Rearranging the equation gives:
θ=5λ2d
In the geometry of the setup, the y-coordinate of the minima can be expressed as:
y=Dtan(θ)
For small angles, tan(θ)≈θ. Thus,
y≈Dθ
Substituting the expression for θ:
y≈D(5λ2d)
This gives:
y=5Dλ2d
Since minima can occur above and below the central maxima, the y-coordinates for the third minima are:
y=±5Dλ2d
The y-coordinates of the third minima are:
y=5Dλ2dandy=−5Dλ2d
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - LEVEL 2 (single correct option)
1 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 More Than One Correct
6 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Subjective Questions
5 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
Let S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
View SolutionIn a Young's double slit experiment, the slit separation is 1mm and the screen is 1m from the slit. For a monochromatic light of wavelength 500nm, the distance of 3rd minima from the central maxima is
View Solution
Knowledge Check
In a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
AλθBλθC2λθDλ2θ
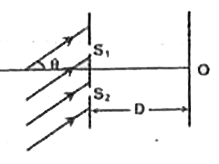
In Young's double slit experiment parallel monochromatic light is incident on both the slits at an angle as shown in the figure. To obtain the central maxima at on the screen we can
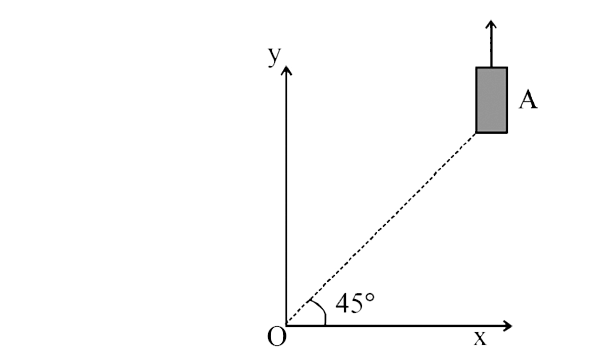
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
View SolutionIf the intensity of light in double slit experiment from slit 1 and slit 2 are l0 and 25l0 respectively, find the ratio of intensities of light at minima and maxima in the interference pattern.
View SolutionIf the separation between slits in Young’s double slit experiment is reduced to 13 rd, the fringe width becomes n times. The value of n
View SolutionIn Young's double-slit experiment, two wavelengths of light are used simultaneously where λ2=2λ1. In the fringe pattern observed on the screen,
View SolutionIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
View SolutionThe Young's double slit experiment is performed with blue light and green light of wavelength 4360Å and 5460Å respectively. If y is the distance of 4th maxima from the central one, then
View Solution
