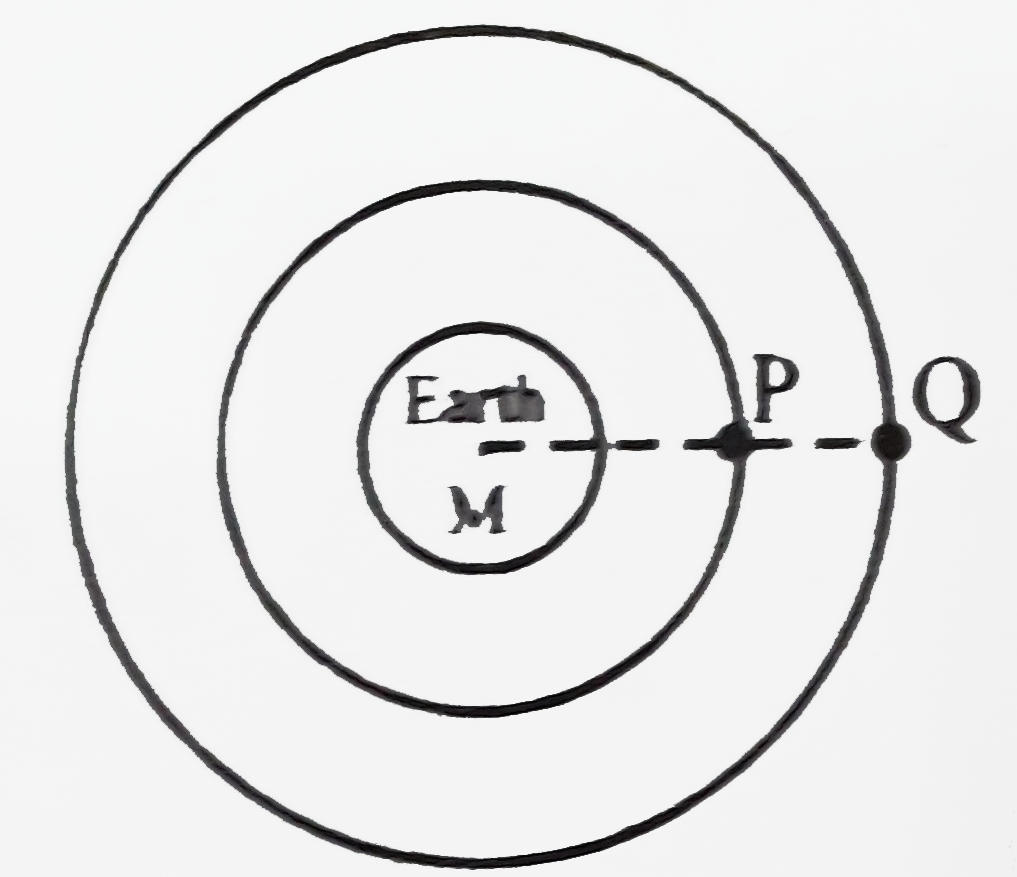
A satellite $P$ is revolving around the earth at a height $h$ =radius of earth $(R)$ above equator. Another satellite $Q$ is at a height $2 h$ revolving in oppisite direction. At an instant the two are at same vertical line passing through centres of sphere. Find the least time of after which again they are in this situation.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{2 π R^{3 / 2} 6 \sqrt{6}}{\sqrt{G M} (2 \sqrt{2} + 3 \sqrt{3})}$

Average velocity of satellite P,
$W_{p} = \frac{V_{P}}{2 R} = \frac{1}{2 R} \sqrt{\frac{G M}{2 R}}$
Average velocity of satellite Q
$W_{Q} = \frac{V_{Q}}{3 R} = \frac{1}{3 R} \sqrt{\frac{G M}{3 R}}$
Least time when P and Q will be in same vertical line
$= \frac{2 π}{ω_{1}} + \frac{2 π}{ω_{2}} = \frac{2 π R^{3 / 2} 6 \sqrt{6}}{\sqrt{G M} (2 \sqrt{2} + 3 \sqrt{3})}$

Updated on:21/07/2023

|

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

ALLEN-GRAVITATION-Exercise 4 B (Brain Storming Subjective Exercise)

Home
Ask Doubt
Profile