The earth may be regarded as a spherically shaped uniform core of density ρ1 and radius R2 surrounded by a uniform shell of thickness R2 and density ρ2. Find the ratio of ρ1ρ2 if the value of acceleration due to gravity is the same at surface as at depth R2 from the surface.
The correct Answer is:73
To solve the problem, we need to find the ratio of the densities ρ1ρ2 given that the acceleration due to gravity is the same at the surface of the Earth and at a depth of R2 from the surface.
1. Understanding the Structure of the Earth:
- The Earth consists of a uniform core of radius R2 and density ρ1.
- It is surrounded by a uniform shell of thickness R2 and density ρ2.
- Therefore, the outer radius of the Earth is R.
2. Acceleration due to Gravity at the Surface:
- The formula for gravitational acceleration at the surface of a sphere is given by:
gsurface=GMR2
- The mass M of the Earth can be expressed as the sum of the mass of the core and the mass of the shell:
M=Mcore+Mshell=(43π(R2)3ρ1)+(43π(R3−(R2)3)ρ2)
3. Calculating Masses:
- The mass of the core:
Mcore=43π(R2)3ρ1=43πR38ρ1=πR3ρ16
- The mass of the shell:
Mshell=43π(R3−(R2)3)ρ2=43π(R3−R38)ρ2=43π(7R38)ρ2=7πR3ρ26
4. Total Mass:
- Therefore, the total mass M becomes:
M=πR3ρ16+7πR3ρ26=πR36(ρ1+7ρ2)
5. Gravitational Acceleration at Depth R2:
- The gravitational acceleration at a depth d=R2 can be calculated using:
gdepth=GMcore(R−d)2=G⋅Mcore(R2)2
- Since Mcore=πR3ρ16:
gdepth=G⋅πR3ρ16(R2)2=G⋅πR3ρ16R24=4GπRρ16
6. Setting Accelerations Equal:
- Since gsurface=gdepth:
GMR2=4GπRρ16
- Substituting M:
G⋅πR36(ρ1+7ρ2)R2=4GπRρ16
- Canceling G and π:
R(ρ1+7ρ2)6=4Rρ16
- Simplifying gives:
ρ1+7ρ2=4ρ1
- Rearranging leads to:
3ρ1=7ρ2⇒ρ1ρ2=73
Final Answer:
The ratio of the densities is:
ρ1ρ2=73
- The Earth consists of a uniform core of radius R2 and density ρ1.
- It is surrounded by a uniform shell of thickness R2 and density ρ2.
- Therefore, the outer radius of the Earth is R.
- The formula for gravitational acceleration at the surface of a sphere is given by:
gsurface=GMR2
- The mass M of the Earth can be expressed as the sum of the mass of the core and the mass of the shell:
M=Mcore+Mshell=(43π(R2)3ρ1)+(43π(R3−(R2)3)ρ2)
- The mass of the core:
Mcore=43π(R2)3ρ1=43πR38ρ1=πR3ρ16
- The mass of the shell:
Mshell=43π(R3−(R2)3)ρ2=43π(R3−R38)ρ2=43π(7R38)ρ2=7πR3ρ26
- Therefore, the total mass M becomes:
M=πR3ρ16+7πR3ρ26=πR36(ρ1+7ρ2)
- The gravitational acceleration at a depth d=R2 can be calculated using:
gdepth=GMcore(R−d)2=G⋅Mcore(R2)2
- Since Mcore=πR3ρ16:
gdepth=G⋅πR3ρ16(R2)2=G⋅πR3ρ16R24=4GπRρ16
- Since gsurface=gdepth:
GMR2=4GπRρ16
- Substituting M:
G⋅πR36(ρ1+7ρ2)R2=4GπRρ16
- Canceling G and π:
R(ρ1+7ρ2)6=4Rρ16
- Simplifying gives:
ρ1+7ρ2=4ρ1
- Rearranging leads to:
3ρ1=7ρ2⇒ρ1ρ2=73
The ratio of the densities is:
ρ1ρ2=73
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 4 B (Brain Storming Subjective Exercise)
20 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 5 A (Previous Year Questions)
26 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)
20 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
The acceleration due to gravity at a depth R/2 below the surface of the earth is
View SolutionA planet is made of two materials of density ρ1 and ρ2 as shown in figure. The acceleration due to gravity at surface of planet is same as a depth 'R'. The ratio of ρ1ρ2 is x3. Find the value of x.

View Solution
Knowledge Check
The radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2.The ratio of the accelerations due to gravity at their surface is
AR1ρ2R2ρ1BR1ρ1R2ρ2Cρ1R22ρ2R21DR1R2ρ1ρ2The density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the ratio of ρ1ρ2
 A2.3B4.5C3.2D5.4
A2.3B4.5C3.2D5.4
A solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?

View SolutionThe density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the ratio of ρ1ρ2

View SolutionThe density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the radio of ρ1ρ2

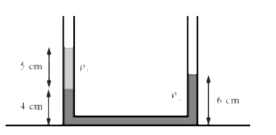
View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
View SolutionA solid ball of radius R has a charge density ρ given by ρ=ρ0(1−rR)for0≤r≤R The electric field outside the ball is :
View SolutionThe density of the core of a planet is x and that of outer shell is y. The radii of the core and that of the planet are R and 2R. The acceleration due to gravity at the surface of planet is same as at a depth R. The ratio of x and y is n/3. Find the value of n.
View Solution
