Two point like objects each with mass m are connected by a massless rope of length l the object are suspended vertically near the surface of earth, so that one object hanging below the other then the objects are relased. Show that the tension in the rope is T=GMmlR3 where M is the mass of the earth and R is its radius |l<<R|
The correct Answer is:n/a
To solve the problem, we need to analyze the forces acting on the two masses connected by a rope and derive the expression for the tension in the rope.
1. Identify the System: We have two masses m connected by a massless rope of length l. The masses are suspended vertically, with one mass hanging below the other.
2. Understand the Gravitational Acceleration: The gravitational acceleration g at the surface of the Earth is given by:
g=GMR2
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
3. Consider the Height Change: When the two masses are at a distance l apart, the upper mass experiences a slightly reduced gravitational acceleration due to the distance from the center of the Earth. The gravitational acceleration at height l can be approximated as:
g′=g(1−lR)≈g−glR
(using the binomial approximation for small l compared to R).
4. Set Up the Force Equations:
- For the lower mass (mass m):
mg−T=ma(1)
- For the upper mass (mass m):
T−mg′=ma(2)
5. Substituting g′: Substitute g′ into equation (2):
T−(g−glR)m=ma
Simplifying this gives:
T=mg−ma+mglR
6. Equate the Two Equations: From equations (1) and (2), we can equate the expressions for T:
mg−ma=T=mg−ma+mglR
Rearranging gives:
2T=mg−mg′=mg−(g−glR)m=mglR
7. Solve for Tension T:
T=mgl2R
8. Substituting for g: Now substitute g=GMR2 into the equation for T:
T=m(GMR2)l2R=GMml2R3
9. Final Expression: Thus, we arrive at the final expression for the tension in the rope:
T=GMmlR3
g=GMR2
where G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
g′=g(1−lR)≈g−glR
(using the binomial approximation for small l compared to R).
- For the lower mass (mass m):
mg−T=ma(1)
- For the upper mass (mass m):
T−mg′=ma(2)
T−(g−glR)m=ma
Simplifying this gives:
T=mg−ma+mglR
mg−ma=T=mg−ma+mglR
Rearranging gives:
2T=mg−mg′=mg−(g−glR)m=mglR
T=mgl2R
T=m(GMR2)l2R=GMml2R3
T=GMmlR3
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 4 B (Brain Storming Subjective Exercise)
20 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 5 A (Previous Year Questions)
26 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)
20 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
If an object of mass m is taken from the surface of earth (radius R) to a height 5R, then the work done is
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View Solution
Knowledge Check
A larger spherical mass M is fixed at one position and two identical point masses m are kept on a line passing through the centre of M. The point masses are connected by rigid massless rod of length l and this assembly is free to move along the line connecting them. All three masses interact only throght their mutual gravitational interaction. When the point mass nearer to M is at a distance r =3l form M, the tensin in the rod is zero for m=k(M288). The value of k is
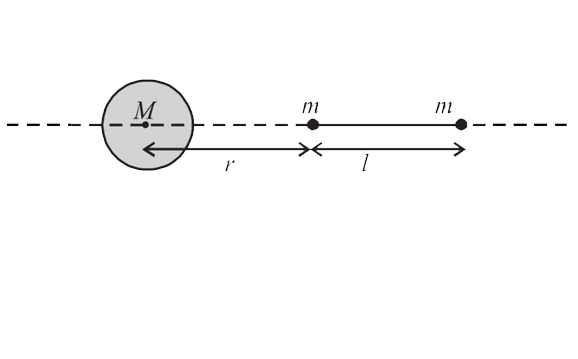 A5B6C7D8
A5B6C7D8
A chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View SolutionA small object of mass m, on the end of a light cord, is held horizontally at a distance r from a fixed support as shown. The object is then released. What is the tension in the cord when the object is at the lowest point of its swing?

View SolutionShow that if a body be projected vertically upward from the surface of the earth so as to reach a height nR above the surface
(i) the increase in its potential energy is (nn+1)mgR,
(ii) the velocity with it must be projected is √2ngRn+1, where r is the radius of the earth and m the mass of body.
View SolutionAn object is projected in upward direction with speed √gR6 from height h= 2R above the surface of earth. The speed with which the object will collide the earth surface. (Neglect the air drag, R us the radius of the earth and M is mass of earth
View SolutionA uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
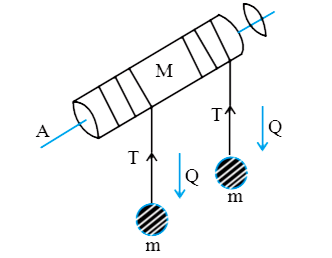
View SolutionAn object of mass m is raised from the surface of the earth to a height equal to the radius of the earth, that is, taken from a distance R to 2R from the centre of the earth. What is the gain in its potential energy ?
View SolutionTwo metallic balls of mass m are suspended by two strings of length L. The distance between upper ends is L. The angle at which the string will be inclined with vertical due to attraction is (m<<M where M is the mass of Earth)
View Solution
