Two equal masses each in are hung from a balance whose scale pans differ in vertical height by h. The error in weighing in terms of density of the earth ρ is
πGρmh
13Gρmh
83πGρmh
43πGρmh
To solve the problem, we need to find the error in weighing two equal masses when they are hung from a balance with a height difference h between the scale pans. Here’s a step-by-step solution:
Step 1: Understand the Weights
Let the mass of each object be m. The weight of the first mass at the surface of the Earth is given by:
W1=mg
where g is the acceleration due to gravity at the surface.
Step 2: Weight at Height h
For the second mass that is at a height h, the weight W2 can be expressed using the formula for gravitational acceleration at height h:
gh=g(1−2hr)
where r is the radius of the Earth. Therefore, the weight at height h is:
W2=mgh=m⋅g(1−2hr)
Step 3: Calculate the Difference in Weights
The difference in the readings of the balance (error in weighing) is given by:
ΔW=W1−W2
Substituting the expressions for W1 and W2:
ΔW=mg−m⋅g(1−2hr)
ΔW=mg−mg+2mghr
ΔW=2mghr
Step 4: Express g in Terms of Density
We know that the acceleration due to gravity g can also be expressed in terms of the density of the Earth ρ:
g=GMr2
where M is the mass of the Earth. The mass of the Earth can be expressed in terms of its density:
M=ρ⋅V=ρ⋅43πr3
Substituting this into the equation for g:
g=G(ρ⋅43πr3)r2=43Gρπr
Step 5: Substitute g Back into the Error Equation
Now substitute g back into the expression for ΔW:
ΔW=2mhr⋅43Gρπr
The r cancels out:
ΔW=83πGρmh
Final Answer
Thus, the error in weighing in terms of the density of the Earth ρ is:
ΔW=83πGρmh
Let the mass of each object be m. The weight of the first mass at the surface of the Earth is given by:
W1=mg
where g is the acceleration due to gravity at the surface.
For the second mass that is at a height h, the weight W2 can be expressed using the formula for gravitational acceleration at height h:
gh=g(1−2hr)
where r is the radius of the Earth. Therefore, the weight at height h is:
W2=mgh=m⋅g(1−2hr)
The difference in the readings of the balance (error in weighing) is given by:
ΔW=W1−W2
Substituting the expressions for W1 and W2:
ΔW=mg−m⋅g(1−2hr)
ΔW=mg−mg+2mghr
ΔW=2mghr
We know that the acceleration due to gravity g can also be expressed in terms of the density of the Earth ρ:
g=GMr2
where M is the mass of the Earth. The mass of the Earth can be expressed in terms of its density:
M=ρ⋅V=ρ⋅43πr3
Substituting this into the equation for g:
g=G(ρ⋅43πr3)r2=43Gρπr
Now substitute g back into the expression for ΔW:
ΔW=2mhr⋅43Gρπr
The r cancels out:
ΔW=83πGρmh
Thus, the error in weighing in terms of the density of the Earth ρ is:
ΔW=83πGρmh
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 1 (Check your Grasp)
28 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 2 (Brain Teasers)
27 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
Two identical blocks of mass m are suspended from a beam balance whose scale pans differ in vertical height by h(h<<R), if R and ρ are the radius and density of the earth, then the error in weighing is
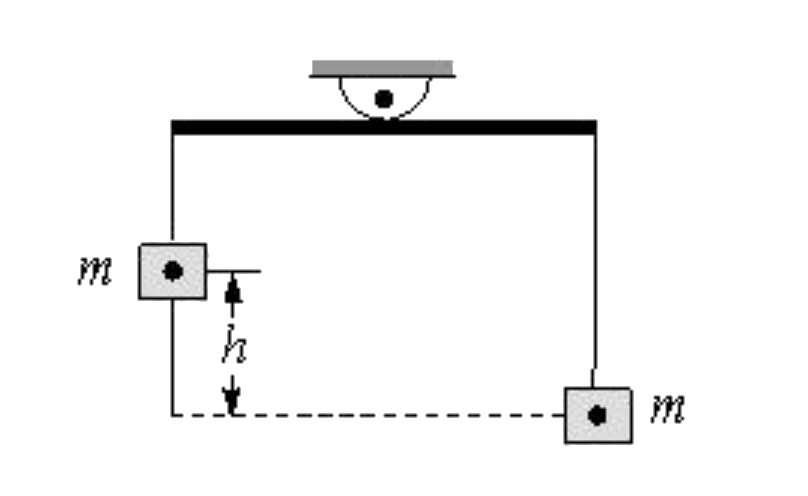
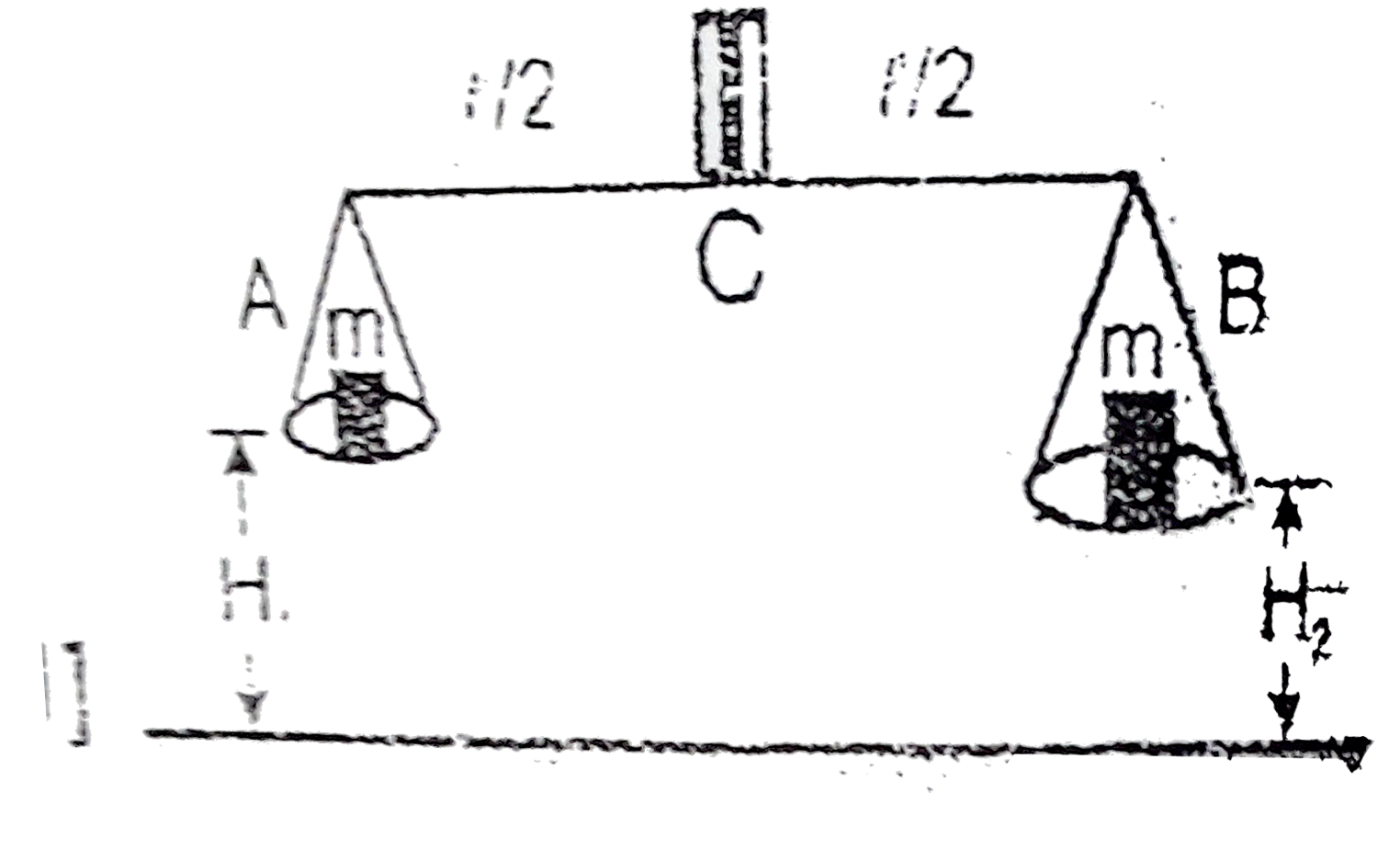
View SolutionTwo blocks of masses m each are hung from a balances as shown in the figure. The scale pan A is at height H1 whereas scale pan B is at height H2 Net torque of weights acting on the system about point C will be (length of the rod is l and H1 & H2 are lt ltR ) (H1>H2)
 .
.
View SolutionTwo objects of equal mass rest on the opposite pans of an arm balance. Does the scale remain balance when it is accelerated up or down in a life ?
View SolutionThere are two bodies A and B of same mass. A is placed near equator of earth and B is placed at a height h above the pole of earth. if both the bodies weighs equally. Find h in terms of radius R of earth, angular speed ω of earth and g acceleration due to gravity close to earth.
View SolutionOn the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
View SolutionTwo vertical plates submerged partially in a wetting liquid form a wedge with a very small angle δφ. The edge of this wedge is vertical. The density of the liquid is ρ, its surface tension is α, the contact angle is θ. Find the height h, to which the liquid rises, as a function of the distance x from the edge.
View SolutionA rock is found to weigh w in air when suspended from a spring scale. When completely submerged in water while attached to the spring scale, it weighs wsubmerged as shown in Fig. Find the density of the rock ρrock in terms of Rock the scale reading and the density of water
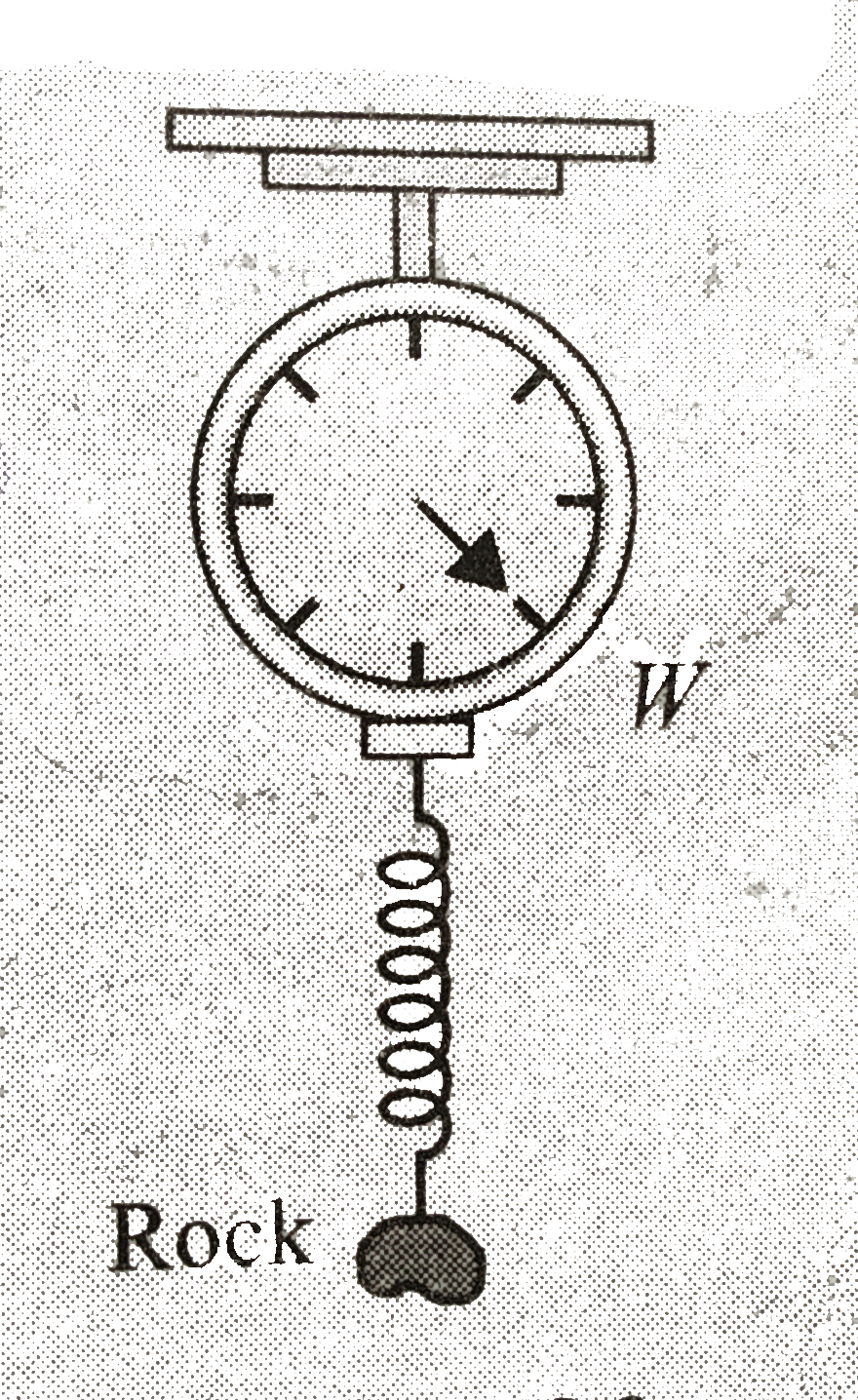
View SolutionThe work done to raise a mass m from the surface of the earth to a height h, which is equal to the radius of the earth, is :
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View Solution
