Derive an expression for magnetic field at the centre of circular current carrying coil. Solution in Punjabi
Consider a current carrying coil carrying current I.
O is the centre of the circular coil and a be its radius.
Consider a point P on the axis of this current carrying circular coil at a distance r from the centre of the coil.
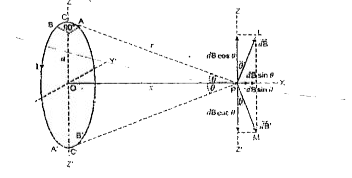
Suppose AB is a small elementary portion of lengthdl at a distance r from the observation point. Every current element is perpendicular to the direction of →r.
According to Biot-Savart.s Law,
Magnetic field at P due to small element AB = dB
and dB=μ04πIdlsinθr2
dB=μ04πIdlr2 [sinθ=sin90∘=1andθ=90∘]
−→dB is perpendicular to the plane in which →dl and →r lie and is along PL which is perpendicular to PC.
Resolve dB into two rectangular components
1. dBcosθ, which is perpendicular to the axis of the coil.
2. dBsinθ, which is along the axis of coil but away from the centre of the coil.
As the coil is symmetrical about its axis, so every element of length →dl has an equal and opposite element, for example, AB has an equal and opposite element A.B. at diametrically opposite point D. The magnetic field −→dB due to the current element A.B. has the magnitude same as that due to the current element AB but its direction is along the PM. Thus,
∣∣∣−→dB∣∣∣=∣∣∣−→dB∣∣∣
Both −→dB and −−→dB. can be resolved in two mutually perpendicular components along PX and YY.. The y -components of the magnetic field due to these elements along YY. being equal and opposite cancel each other. Hence, the resultant of these components (−→dBcos) for the complete loop, from symmetry, is zero. Thus, only the x-component of −→dB=−→dBsinϕ survives and this component of magnetic field due to each component of the loop points in the same direction.
Therefore, magnetic field at point P due to whole coil is equal to the sum of −→dBsinϕ components of magnetic field due to each element, i.e.,
→B=∑−→dBsinϕ
or →B=∫−→dBsinϕ ...(1)
Now, ∣∣∣−→dB∣∣∣ for the current element at P is given by :
dB=μ0I4πdlsinπ2r2 (asθ=90∘)
or dB=μ0Idl4πr2
Substituting this value of dB is eqn. (1), we have
B=∫μ0Idl4πr2sinϕ
=μ0Isinϕ4πr2×2πa
as I,ϕ and r are fixed and
∫dl = Circumference of the coil =2πa
or B=μ04π2πIar2sinϕ (2)
Now from right angld ΔCOP
sinϕ=ar=a√a2+x2asr=√a2+x2
∴B=μ04π2πIar2×a√a2+x2
or B=μ02πI4π×a2(a2+x2)3/2
If there are n turns in the coil, then the strength of magnetic field at point P due to the coil will be n times the magnetic field due to a coil of single turn, i.e.,
B=μ04π2πnI×a2(a2+x2)3/2 ....(3)
If the observation lies at the centre of the coil then x=0
From eqn. (3),
B=μ04π2πnIa2(a2)3/2
B=μ04π2πnIa
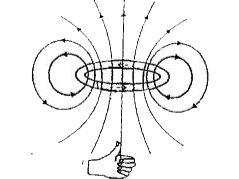
which is required expression for magnetic field at the centre of current carrying circular coil. Magnetic field due to current carrying circular coil can be shown as given aside.
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - NUMERICALS PROBLEMS3videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - SHORT ANSWER TYPE QUESTIONS4videos
MAGNETIC EFFECTS OF CURRENT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC DIPOLES AND EARTH'S MAGNETISMEXERCISE - Most Expected Questions8videos
MAGNETIC DIPOLES AND EARTH'S MAGNETISM
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - NUCLEAR REACTIONSEXERCISE - Numerical Problems9videos
NUCLEAR REACTIONS
Similar Questions
A current of 15A flows through a coil Magnetic field at centre of semi-circular loop of 5.0 cm radius as shown in fig. Find out the direction and magnitude of magnetic field at the centre of the arc.
 01:53View Solution
01:53View SolutionExplain Biot-Savart law for the magnetic field produced at a point due to the current flowing in a current element. How will you determine the direction of the field?
07:42View SolutionWhat do you mean by Neutral Point in a magnetic field?
13:28View SolutionIt is given that each fission of a chain reaction produces 200 MeV energy. What is the number of fissions taking place per second it the reactor produces 1012W Power ?
05:16View SolutionPlot a magnetic field due to a circular coil carrying current and explain the law used to find the direction of magnetic field at the centre of circular coil carrying current.
01:32View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
14:14View SolutionDerive an expression for the magnetic induction at the centre of a current carrying circular coil using Biot-Savart law.
02:59View SolutionWrite the expression for magnetic field at the centre of a current carrying circular coil.
04:30View SolutionUsing Biot - Savart's law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
03:20View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
03:40View SolutionUsing Biot-Savart's law, derive an expression for magnetic field at the centre of a current carrying circular coil. What will be the direction of this magnetic field?
17:36View SolutionDerive an expression for magnetic field at the centre of circular current carrying coil.
05:42View SolutionDerive an expression for the magnetic field.at the centre of a current carrying coil.
02:54View SolutionState the expression for the magnetic field due to a circular are of wire carrying a current I. Hence find the magnetic field at the centre of circular coil and having n turns.
07:35View SolutionDerive an expression for the magnetic field intensity produced at a point lying along the axis of a circular coil carrying current.
04:06View Solution
