Using Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.

Video Solution

Text Solution

Verified by Experts

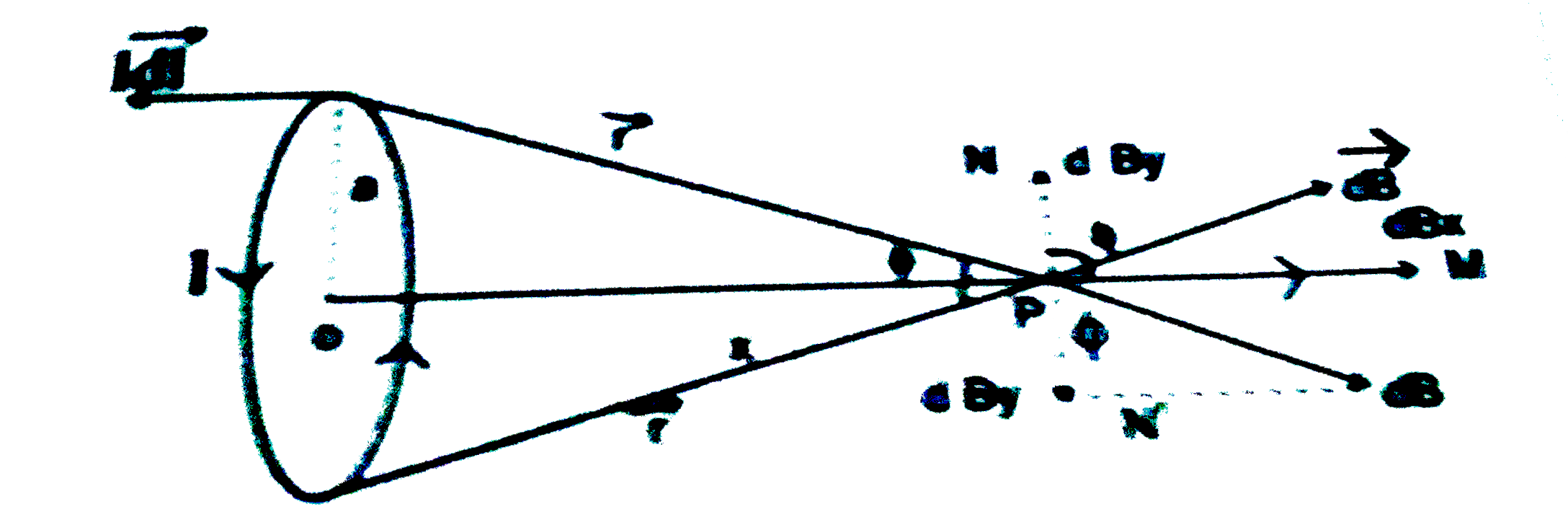
According to Biot-Savart's law, magnetic field due to a current element is given by
$- \to d B = \frac{μ 0}{4 π} \frac{I \to d l X ¯ x}{r^{2}} Where r = \sqrt{x^{2} + a^{2}}$
$∴ d B = \frac{μ 0}{4 π} \frac{I d l sin 90^{\circ}}{x^{2} + e^{2}}$
And direction of $- \to d B is ⊥$ to the plane containing $I \to d l and \to r$ .
Resolving $- \to d B$ alonhg the x-axis and y-axis.
$d B_{x} = d B Sin θ$
$d B_{y} = d B cos θ$
taking the contribution of whole current loop we get
$B_{x} \oint B_{x} = \oint B sin θ = \int \frac{μ 0}{4 π} \frac{1 d l}{x^{2} + a^{2}} \frac{a}{\sqrt{x &^{2} + a^{2}}} .$
$B_{x} = \frac{μ 0}{4 π} \frac{1 n}{{(x^{2} + a^{2})}^{E / Z}} \oint d l = \frac{μ 0}{4 π} \frac{ln \times 2 π a}{{(x^{2} + a^{2})}^{E / Z}}$
$And B_{y} = \oint d B_{y} = \oint d B cos θ = 0$
$∴ B_{p} = \sqrt{B_{x}^{2} + B_{y}^{2}} = B_{x} = \frac{μ 0}{4 π} \frac{2 I A}{{(x^{2} + a^{2})}^{E / Z}}$
$∴ - \to B_{p} = \frac{μ 0}{4 π} \frac{2 m}{(x^{2} + a^{2})} (∵ \to m = I A)$
For centre x = 0
$∴ ∣ ∣ ∣ - \to B_{0} ∣ ∣ ∣ = \frac{μ 0}{4 π} \frac{2 I π a^{2}}{a^{2}} = μ 0 (\frac{l}{2 a}) in the direction of \to m$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

XII BOARD PREVIOUS YEAR PAPER ENGLISH-SAMPLE PAPER 2019-SECTION C

Home
Ask Doubt
Profile