Write expression for the magnetic flux density at a point due to a current carrying wire of:
a finite length?Solution in Punjabi
Consider a long straight wire LM.
Let I = Current flowing through the wire from L to M.
Let P be the observation point, where we want to calculate the magnetic field.
OP = a = Perpendicular distance of P from the current carrying wire
Consider the small element CD of length dl of the wire and I is distance of mid-point of elementary portion CD from O.
r=OʻP = Distance of mid-point of small elementary portion CD from P.
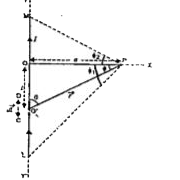
0 = Angle between the current carrying wire and the line joining the mid-point of CD to P, i.e., between →dl and →r .
According to Biot-Savart.s law, magnetic induction −→dB at the point P due to small current element CD is given by
−→dB=μ04πI→dl׈rr2
In magnitude dB=μ04πIdlsinθr2 ...(1)
and sinθ=dr=cosθ .....(2)
or r=acosϕ=asecϕ ....(3)
Also , tanϕ=l/aorl=atanϕ ....(4)
dl=asec2ϕdϕ
Substituting the values from eqns. (2), (3) and (4) in eqn. (1), we get
dB=μ04πI(asec2ϕdϕ)cosϕa2sec2ϕ
dB=μ0I4πacosϕdϕ ....(5)
Join PM and PL. Let ∠OPM.=ϕ2 and ∠OPL=−ϕ1
Then, magnetic field due to the whole length of conductor LM can be calculated by integrating eqn. (5) within the limits −ϕ1 to −ϕ2. Thus,
B=∫ϕ2−ϕ1dB=μ0I4πa∫ϕ2−ϕ1cosϕdϕ
=μ0I4πa[sinϕ]−θ2−θ1=μ0I4πa[sinϕ2−sin(ϕ1)]
=μ0I4πa[sinϕ2+sinϕ1] ....(6)
The above expression gives the magnitude of the magnetic field due to current carrying straight conductor of finite length.
If the conductor is infinitely long and the point P lies near the centre of the conductor, then
ϕ1=ϕ2=π2
So, B=μ0I4πa[sinπ2+sinπ2]
B=μ02I4πa
It is the expression for magnetic field due to an infinitely long current carrying straight conductor.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENTBOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - NUMERICALS PROBLEMS
3 Videos
- MAGNETIC EFFECTS OF CURRENTBOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF CURRENTEXERCISE - SHORT ANSWER TYPE QUESTIONS
4 Videos
- MAGNETIC DIPOLES AND EARTH'S MAGNETISMBOOK - BETTER CHOICE PUBLICATIONCHAPTER - MAGNETIC DIPOLES AND EARTH'S MAGNETISMEXERCISE - Most Expected Questions
8 Videos
- NUCLEAR REACTIONSBOOK - BETTER CHOICE PUBLICATIONCHAPTER - NUCLEAR REACTIONSEXERCISE - Numerical Problems
9 Videos
Similar Questions
A current of 15A flows through a coil Magnetic field at centre of semi-circular loop of 5.0 cm radius as shown in fig. Find out the direction and magnitude of magnetic field at the centre of the arc.

View SolutionExplain Biot-Savart law for the magnetic field produced at a point due to the current flowing in a current element. How will you determine the direction of the field?
View SolutionWhat do you mean by Neutral Point in a magnetic field?
View SolutionIt is given that each fission of a chain reaction produces 200 MeV energy. What is the number of fissions taking place per second it the reactor produces 1012W Power ?
View SolutionConsider the magnetic field produced by a finitely long current carrying wire .
View SolutionThe magnetic induction at any point due to a long straight wire carrying a current is
View SolutionThe direction of magnetic field at a point due to an infinitely long wire carrying current is
View SolutionWrite the expression for magnetic flux at one end of a long solenoid carrying current.
View SolutionGive the expression for magnetic flux density, at a point on the axis, due to a current carrying circular conductor.
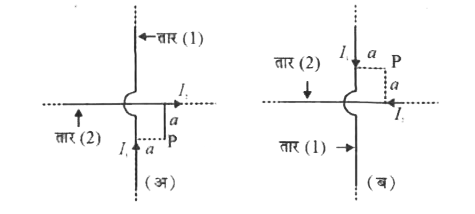
View Solutionचित्र में प्रदर्शित दो अनन्त लम्बाई के धारावाही चालक तारों के कारण बिंदु P पर परिणामी चुम्बकीय क्षेत्र ज्ञात कीजिए।
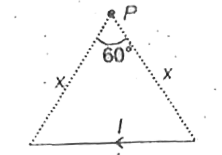
View SolutionA straight wire of finite length carrying current I subtends an angle of 60∘ at point P as shown. The magnetic field at P is
View SolutionStatement-1: Ampere's law cannot be used determine magnetic field due a current carrying wire of finite length Statement-2: Ampere's law is not valid for wires finite length
View SolutionWrite formula of the magnetic field at r perpendicular distance for finite current carrying wire.
View Solutionपरिमित लम्बाई के तार के कारण बिन्दु 'P' पर चुम्बकीय क्षेत्र होगा
View SolutionMagnetic Field Due to Current Carrying Wire
View SolutionIntroduction|Magnetic Effect due to Current Carrying Wire
View Solution
