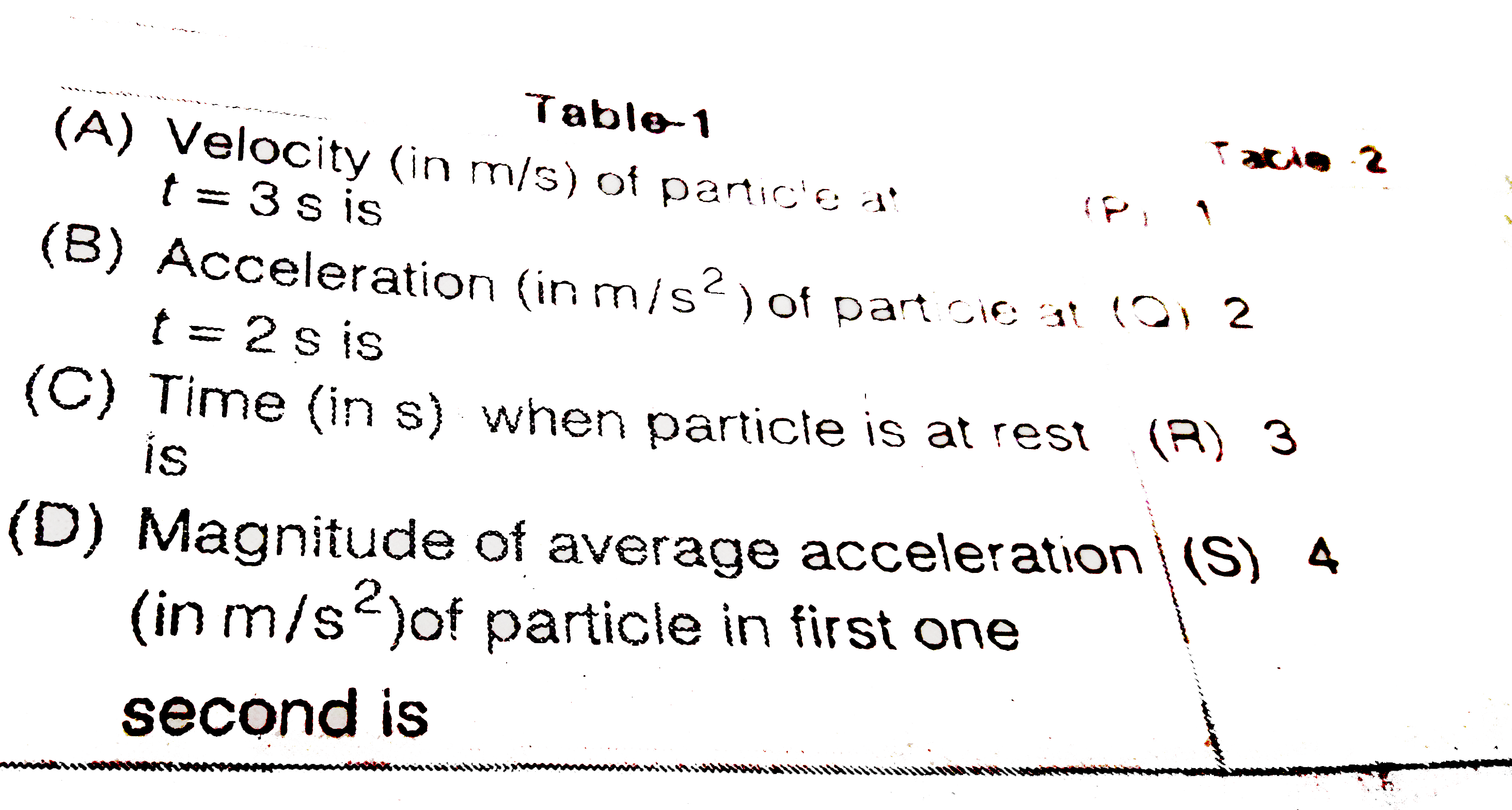The velocity of a particle moving along a straight line is given by the relation v2=ax2+2bx+c. The acceleration varies as ...........
The correct Answer is:T
To find the relation of acceleration based on the given velocity equation v2=ax2+2bx+c, we can follow these steps:
1. Identify the given equation:
We start with the equation for velocity:
v2=ax2+2bx+c
2. Differentiate with respect to time:
To find acceleration, we need to differentiate the velocity with respect to time. Since v is a function of x, we apply the chain rule:
dvdt=dvdx⋅dxdt
Here, dxdt=v (the definition of velocity).
3. Differentiate v2:
Differentiate both sides of the equation v2=ax2+2bx+c with respect to x:
d(v2)dx=d(ax2+2bx+c)dx
Using the chain rule on the left side:
2vdvdx=2ax+2b
4. Solve for dvdx:
Rearranging the equation gives:
dvdx=2ax+2b2v=ax+bv
5. Substitute dvdx into the acceleration formula:
Now, substituting back into the acceleration formula:
a=dvdt=dvdx⋅dxdt=dvdx⋅v
This gives:
a=(ax+bv)⋅v=ax+b
6. Final expression for acceleration:
Therefore, the acceleration a varies as:
a=ax+b
Final Result:
The acceleration varies as ax+b.
We start with the equation for velocity:
v2=ax2+2bx+c
To find acceleration, we need to differentiate the velocity with respect to time. Since v is a function of x, we apply the chain rule:
dvdt=dvdx⋅dxdt
Here, dxdt=v (the definition of velocity).
Differentiate both sides of the equation v2=ax2+2bx+c with respect to x:
d(v2)dx=d(ax2+2bx+c)dx
Using the chain rule on the left side:
2vdvdx=2ax+2b
Rearranging the equation gives:
dvdx=2ax+2b2v=ax+bv
Now, substituting back into the acceleration formula:
a=dvdt=dvdx⋅dxdt=dvdx⋅v
This gives:
a=(ax+bv)⋅v=ax+b
Therefore, the acceleration a varies as:
a=ax+b
The acceleration varies as ax+b.
Similar Questions
Knowledge Check
A particle is moving along a straight line.
AIf the acceleration of the particle is more than that of another object, the particle is moving faster.BIf the acceleration is positive, the speed must be increasing.CIf the acceleration and the velocity have the same sign, the speed must be increasing.DIf the acceleration is zero, the velocity is constant but the speed may be changing.The variation of velocity of a particle moving along a straight line is shown in . is
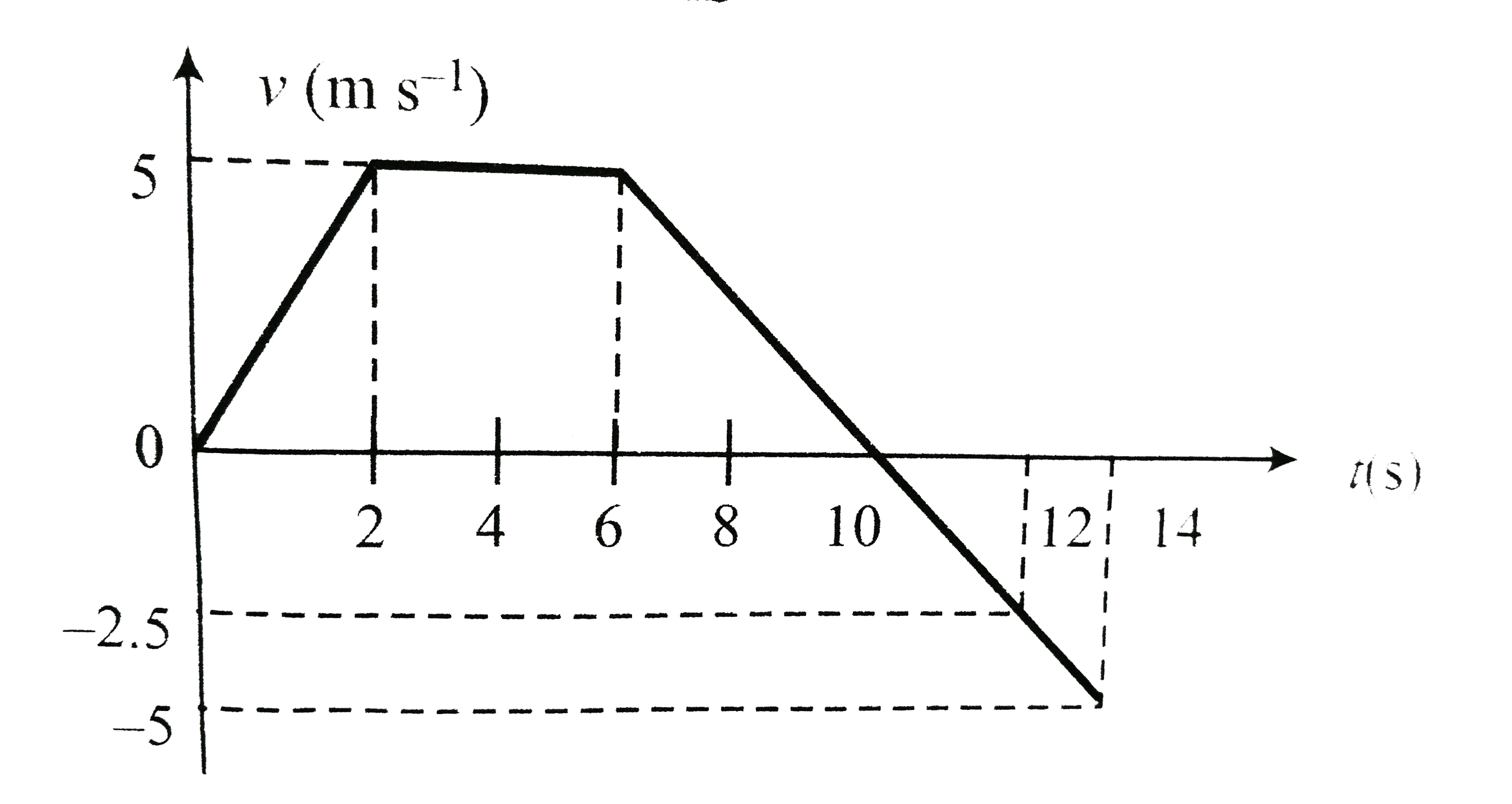 .A37.5kmB32.5mC35.0mDNone of these
.A37.5kmB32.5mC35.0mDNone of theseThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
AxbBxabCabxDax
Position of a particle moving along a straight line is given by x=2t2+t . Find the velocity at t = 2 sec.
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2, where x is its distance from the origin. The acceleration of the particle is
View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :

View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 (where x is its distance from the origin). The acceleration of the particle is
View SolutionThe acceleration of a particle moving in straight line is defined by the relation a=−4x(−1+14x2), where a is acceleration in m/s2 and x is position in meter. If velocity v=17m/s when x=0, then the velocity of the particle when x=4 meter is :
View Solution