If the velocity v of a particle moving along a straight line and its distance s from a fixed point on the line are related by v2=a2+s2, then its acceleration equals
as
s
s2
2s
The correct Answer is:B
Step by step video, text & image solution for If the velocity v of a particle moving along a straight line and its distance s from a fixed point on the line are related by v^(2)=a^(2)+s^(2), then its acceleration equals by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Section I - Solved Mcqs27videos
DERIVATIVE AS A RATE MEASURER
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Chapter Test30videos
DIFFERENTIAL EQUATIONS
Similar Questions
The speed (v) of particle moving along a straight line, when it is of a distance (x) from a fixed point on the line, is given by : v2=144−9x2
_S01_056_Q01.png)
View SolutionThe distance covered by a particle moving in a straight line from a fixed point on the line is s, where s2=at2+2bt+⋅ Then prove that acceleration is proportional to s−3.
View Solution
Knowledge Check
- Question 1 - Select One or More
The speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v2=144−9x2. Select the correct alternatives
AThe motioni of the particle is SHM with time period T=2π3 unitsBThe maximum displacement of the particle from the fixed point is 4 unitsCThe magnitude of acceleration at a distance 3 units from the fixed point is 27 unitsDthe motion of the particles is periodic but not simple harmonic - Question 2 - Select One
If a particle moving in a straight line and its distance x cms from a fixed point O on the line is given by x=√1+t2 cms, then acceleration of the particle at t sec. is
A1x2 cm/sec2B−1x2 cm/sec2C1x3 cm/sec2D−1x3 cm/sec2 - Question 3 - Select One
A particle is moving on a straight line and its distance x cms from a fixed point O on the line is given byx=√t2+1 then the velocity of particle at t=1 is
A1√2B1√3C12√2D13√2
If the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionSpeed v of a particle moving along a straight line, when it is a distance X from a fixed point on the line is given by V2=108−9X2 (all quantities in S.I. unit). Then
View SolutionThe speed v of a particle moving along a straight line, when it is at a distance (x) from a fixed point of the line is given by v2=108−9x2 (all equation are in CGS units):
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
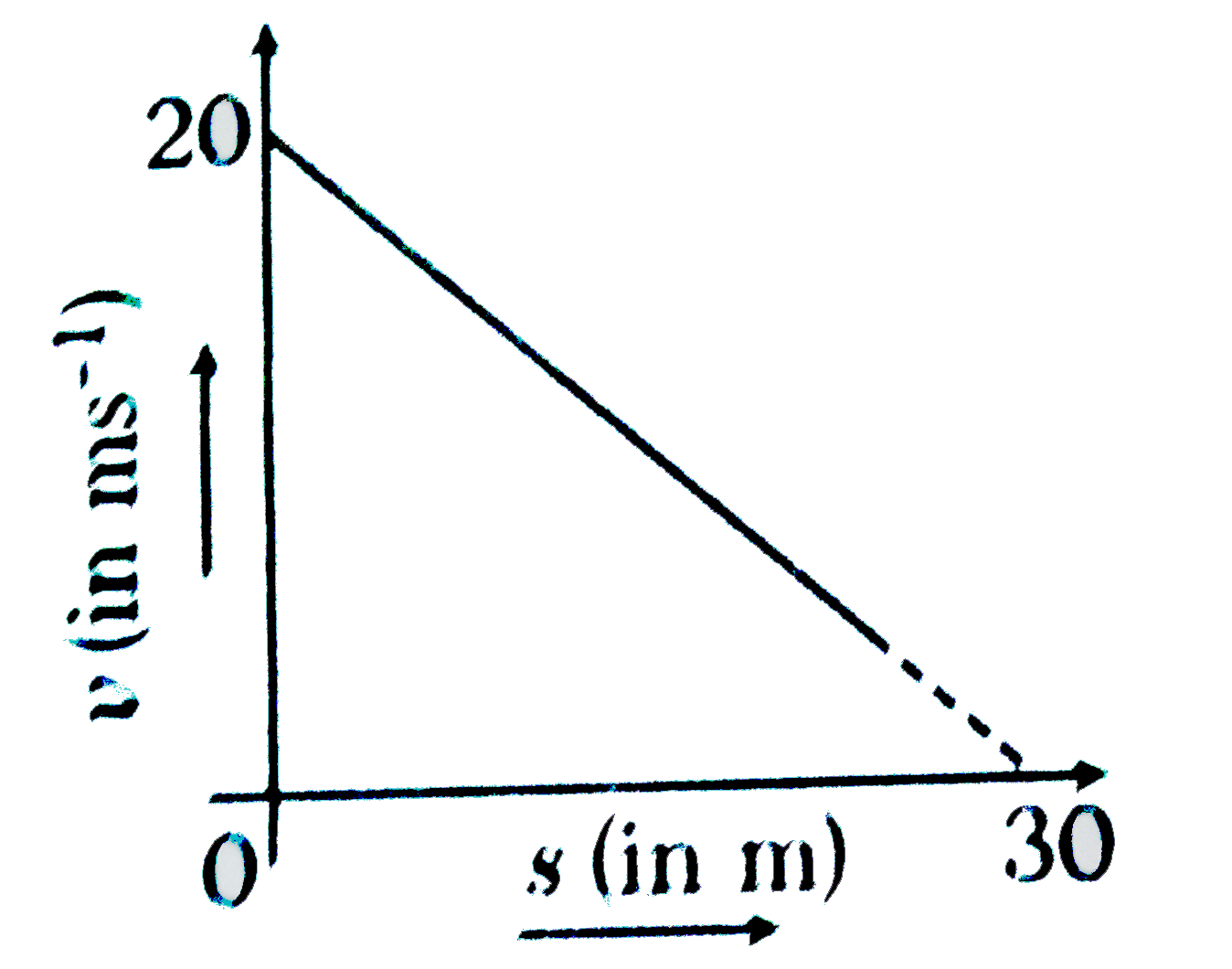
View SolutionThe law of motion of a body moving along a straight line is x=12vt, x being its distance from a fixed point on the line at time t and v is its velocity there. Then
View Solution