The acceleration of a particle moving in straight line is defined by the relation a=−4x(−1+14x2), where a is acceleration in m/s2 and x is position in meter. If velocity v=17m/s when x=0, then the velocity of the particle when x=4 meter is :
12m/s
15m/s
20m/s
25m/s
The correct Answer is:B
The acceleration ……………
a=−4x(−1+0.25x2)
∫v17vdv=∫40(4x−x3)dx
12(v2−172)=42(x2)40−14(x4)40
v2−172=4(42)−12(44)=64−128
V2=298−64=225,V=15m/sec
Similar Questions
The displacement of a particle moving in a straight line is given by s=t3−6t2+3t+4 meters.The velocity when acceleration is zero is "
View SolutionThe acceleration of a particle is given by the relation as a=−kv5/2 , where is a constant. The particle starts at x=0 with a velocity of 16 m/s, and when x = 6, the velocity is observed to be 4 m/s. Find the velocity of particle when x=5m and the time at which the velocity ofthe particle is 9 m/s.
View Solution
Knowledge Check
The motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at the origin .A1 , 0 , 4B1 , 4 , 0C10 , 14 , −34D10 , −1 , 0Acceleration of a particle moving along the x-axis is defined by the law a=−4x, where a is in m/s2 and x is in meters. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of its position coordinates.
(b) find its position x as function of time t.
(c) Find the maximum distance it can go away from the origin.Av=2√2−x2Bv=3√1−x2Cv=2√1−x3Dv=2√1−x2The velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :
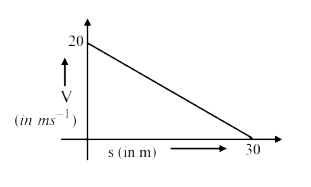 A23ms−2B−23ms−2C203ms−2D−203ms−2
A23ms−2B−23ms−2C203ms−2D−203ms−2
A particle moves in a straight line as s=α(t−4)+β(t−4)2. Find the initial velocity and acceleration.
View SolutionThe position of an object moving on a straight line is defined by the relation x=t3−2t2−4t, where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and
View SolutionA particle moves in a straight line obeying the relation x= t(t-1) where x= displacement in m and t= time in sec.Find the velocity of the particle when its displacement is zero.
View SolutionThe velocity-position graph of a particle moving in a straight line along x -axis is givenbelow.Acceleration of particle,at x=2m is
View SolutionThe velocity-position graph of a particle moving in a straight line along x-axis is given below. Acceleration of particle at x = 2 m is
View Solution
