The velocity of a particle moving on the x-axis is given by v=x2+x, where x is in m and v in m/s. What is its position (in m) when its acceleration is 30m/s2.
The correct Answer is:2
To solve the problem, we need to find the position x when the acceleration a of the particle is 30m/s2. The velocity v is given as a function of position x by the equation:
v=x2+x
Step 1: Express acceleration in terms of position
We know that acceleration can be expressed in terms of velocity and position as follows:
a=vdvdx
Step 2: Differentiate the velocity function
First, we need to differentiate the velocity function v=x2+x with respect to x:
dvdx=ddx(x2+x)=2x+1
Step 3: Substitute v and dvdx into the acceleration formula
Now we can substitute v and dvdx into the acceleration formula:
a=(x2+x)(2x+1)
Step 4: Set the acceleration equal to 30m/s2
We set the expression for acceleration equal to 30:
(x2+x)(2x+1)=30
Step 5: Expand and rearrange the equation
Expanding the left-hand side:
2x3+x2+2x2+x=30
This simplifies to:
2x3+3x2+x−30=0
Step 6: Solve the cubic equation
Now we need to solve the cubic equation 2x3+3x2+x−30=0. We can use trial and error to find rational roots.
1. Testing x=1:
2(1)3+3(1)2+(1)−30=2+3+1−30=−24(not a root)
2. Testing x=2:
2(2)3+3(2)2+(2)−30=16+12+2−30=0(is a root)
Step 7: Conclusion
Thus, we found that x=2 meters is the position when the acceleration is 30m/s2.
Final Answer
The position x when the acceleration is 30m/s2 is:
2m
We know that acceleration can be expressed in terms of velocity and position as follows:
First, we need to differentiate the velocity function v=x2+x with respect to x:
Now we can substitute v and dvdx into the acceleration formula:
We set the expression for acceleration equal to 30:
Expanding the left-hand side:
Now we need to solve the cubic equation 2x3+3x2+x−30=0. We can use trial and error to find rational roots.
2(1)3+3(1)2+(1)−30=2+3+1−30=−24(not a root)
2(2)3+3(2)2+(2)−30=16+12+2−30=0(is a root)
Thus, we found that x=2 meters is the position when the acceleration is 30m/s2.
The position x when the acceleration is 30m/s2 is:
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - H)
Explore 9 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - I)
Explore 3 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - F)
Explore 1 Video
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTEChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
Similar Questions
Knowledge Check
The velocity of a particle moving on the x− axis is gienv by v=x2+x( for x>0) where v is in m/s and x is in m. Find its acceleration in m/s2 when passing through the point x=2m
A0B5C11D30The position of a particle moving on the x-axis is given by x=t3+4t2−2t+5 where x is in meter and t is in seconds
(i) the velocity of the particle at t=4s is 78m/s
(ii) the acceleration of the particle at t=4s is 32m/s2
(iii) the average velocity during the interval t=0 to t=4sis 30m/s
(iv) the average acceleration during the interval t=0 to t=4s is 20m/s2A(i), (ii)B(ii), (iii)C(i), (ii), (iii)DAllvx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
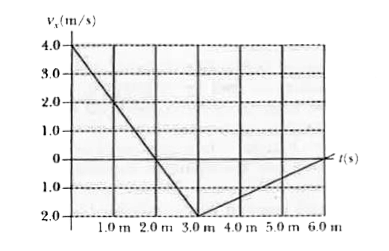 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 m
The velocity (v) of a particle of mass m moving along x-axis is given by v=α√x, where α is a constant. Find work done by force acting on particle during its motion from x=0 to x=2m :-
View SolutionAcceleration of a particle moving along the x-axis is defined by the law a=−4x, where a is in m/s2 and x is in meters. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of its position coordinates.
(b) find its position x as function of time t.
(c) Find the maximum distance it can go away from the origin.
View SolutionThe velocity of a particle moving along x-axis is given as v=x2−5x+4 (in m/s) where x denotes the x-coordinate of the particle in metres. Find the magnitude of acceleration of the particle when the velocity of particle is zero?
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View SolutionVelocity of particle moving along x-axis is given as v=(x3−x2+2) m/sec. Find the acceleration of particle at x=2 meter.
View Solution